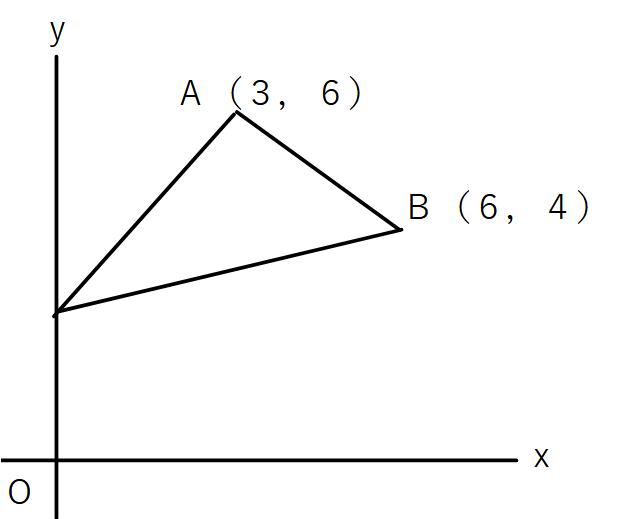
例1)
x軸上に点Pを取って△OAB=△OAPとなるような点Pの座標を求めよ。
※①共通する辺→点辺とみて固定
②この辺と平行で、かつ、向かい合う点を通る直線上にあれば等積変形される
③もう1つの条件(x軸上など)と組み合わせて点を決定する
解)△OAB=△OAP→OAが共通
→共通する辺を底辺とみて等積変形
OAに平行で、かつ点Bを通る直線であれば等積変形される
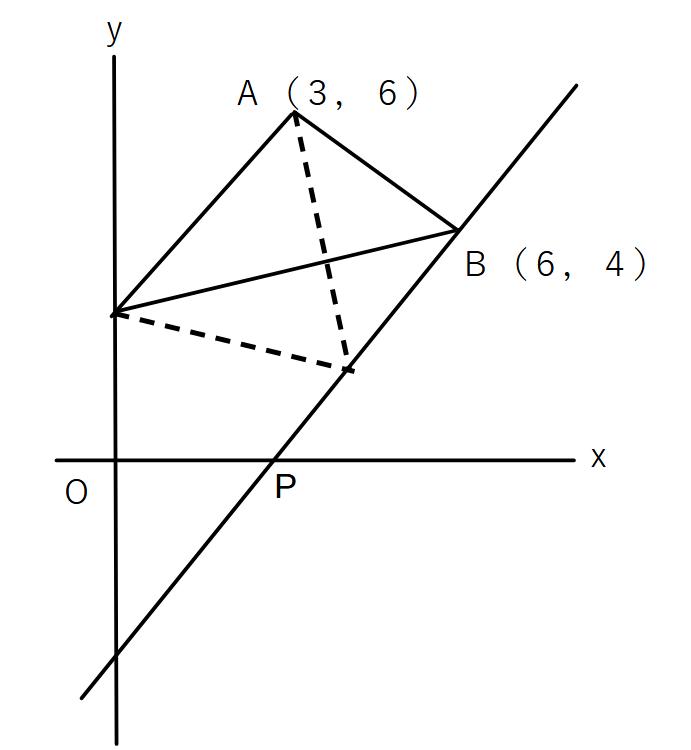
→この直線とx軸との交点が点Pとなる!
直線OAの式
:y=2x →等積変形される直線は傾き2で(6,4)を通る
∴y=2x-8 これとx軸との交点=P(4,0)
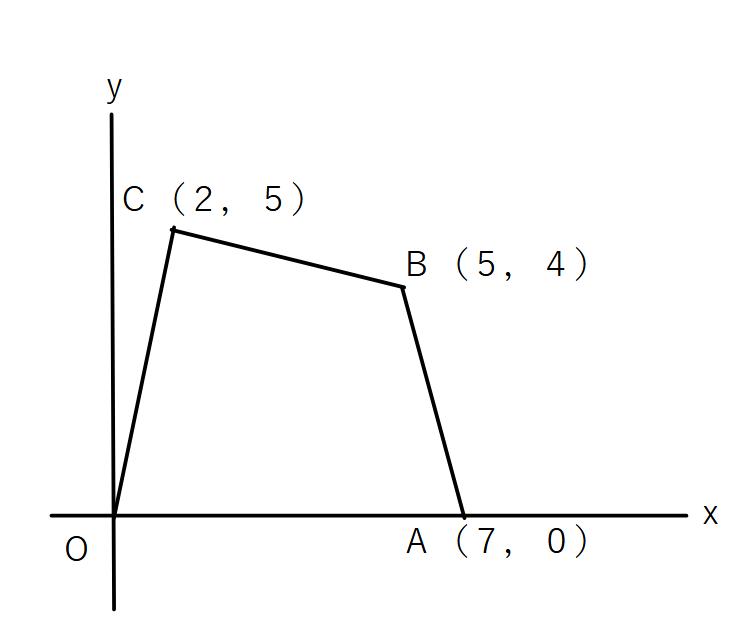
例2)
図の四角形OABCについて
①x軸上に点Dをとり、四角形OABD=△OCDとなるような点Dの座標を求めよ。
②点Cを通り、四角形OABCを二等分する直線の式を求めよ。
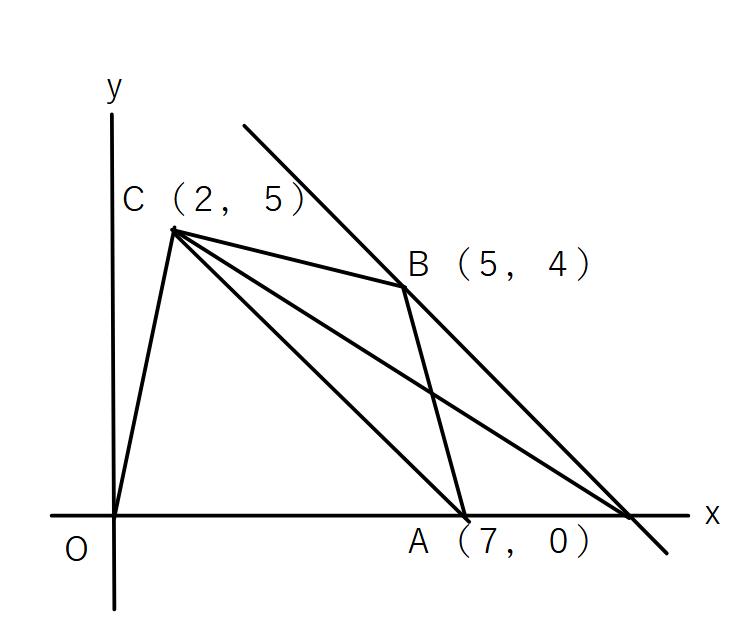
①ACに線を引き、△ABCをACを底辺とみて、等積変形する
直線AC:A(7,0)、C(2,5)を通る→y=ーx+9
点Bを通り、ACに平行な直線を引く
→傾きー1,B(5,4)を通る→y=ーx+9
y=ーx+9とx軸との交点がD
y=0を代入するとx=9
よってD(9,0)
②①より、四角形OABC=△OCD
つまり、点Cを通り△OCDを二等分する直線がそのまま四角形OABCを二等分する
<三角形の二等分>
ある頂点とその向かい合う辺の中点を通る直線は、その三角形を二等分する
点CとODの中点(9/2、0)を通る直線
→求める直線は、y=ー2x+9