(1)平方根
今回からは初めて学ぶ単元「平方根(へいほうこん)」です。

平方根とは、「2乗するとaになる数」と言ったりします。
例えば、図にあるように、3を2乗すると9になります。
同じく、-3を2乗すると9になります。
この関係性を表すとき、「3は9の平方根である」「ー3は9の平方根である」という言い方をするのです。
実際に平方根を求めてみてください。
①9
②100
③1/9
④4/25
⑤144
①\( ±3\)
②\( ±10\)
③\( ±\displaystyle \frac{1}{2}\)
④\( ±\displaystyle \frac{2}{5}\)
⑤\( ±12\)
すぐに回答を入れてしまいましたが、
①これは解説でもあった通り、3とー3が9の平方根であるというそのままです。
②100は10の2乗になりますので、10とー10になります。
③分数ですが、分母と分子でそれぞれ分けて考えていきます。
分子は1なので、1は2乗しても1です。
では分母は、9なので、3とー3になります。それをそのままもどせばよいので、解答通りの形になります。
④③と同様で、分子は4なので2の2乗、分母は25なので5の2乗になり、解答の形になります。
⑤144は12の2乗になりますので、12とー12ということになります。
※ちなみに、11~20くらいまでの2乗の数は覚えておくと何かと楽です。
無理しない程度に覚えておきましょう。
11²=121
12²=144
13²=169
14²=196
15²=225
16²=256
17²=289
18²=324
19²=361
20²=400
(2)√(根号)ルート
平方根は、ある数を2乗にしたらできる数といいました。
図を見てください。
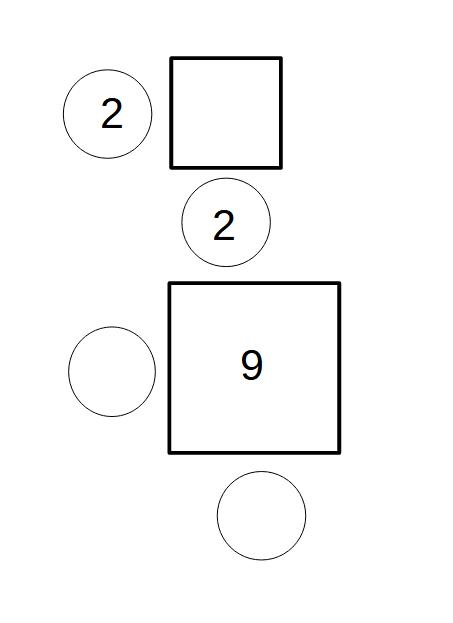
上の正方形は、1辺が2で、面積はいくつでしょうか。
また、下の正方形は、面積が9となっています。
1辺の長さはいくつでしょうか。
お分かりと思いますが、
1辺2の正方形の面積は4
面積9の正方形の1辺は3となります。
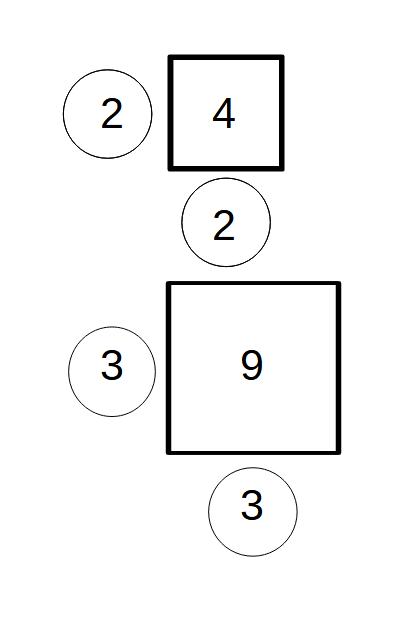
これはそれぞれ、
4の平方根は±2
9の平方根は±3
という、「2乗すれば〇になる」という平方根を表しています。
では、この場合の1辺はどうしましょうか?
今までは2乗すれば〇になる、平方根を表すことができたのですが、これではできません。
なので、次のようにします。
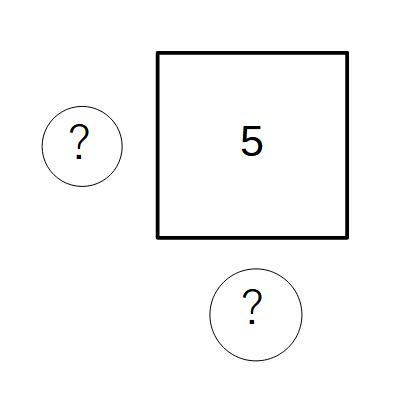
5では1辺を表すことができないので、記号を使って表します。
5の平方根…普通では表せない
↓
\( ±\sqrt{5}\)と表す!\((\sqrt{5})^2=5\)
± √5 と表す!((√ 5)2=5)
√a…2乗するとaになる数
((√ a)2=a)
√…根号、ルートと読みます。
2の平方根…± √2
11の平方根…± √11

(3)√根号のはずし方
4の平方根 …+2 と
…± √4 は同じ
± √4=± √22=±2
√2がきえる!
☆ √ a2=a aは正の数
-√ 32=-3
√ (-3)2=-3…×ダメ √が負はありえない!
=√ 9= √32=3…○OK
☆ルートの中は正にして計算!
問 次の数を求めよ。
①\( \sqrt{3^2} \)
②\( \sqrt{5^2} \)
③\( \sqrt{81} \)
④\( \sqrt{100} \)
⑤\( \sqrt{169} \)
①=3
②=5
③=9
④=10
⑤=13
⑥\( -\sqrt{25} \)
⑦\( -\sqrt{144} \)
⑧\( \sqrt{(-7)^2} \)
⑨\( \sqrt{(-11)^2} \)
⑩\( -\sqrt{(-6)^2} \)
⑥\(=-5\)
⑦\(=-12\)
⑧\(=\sqrt{49}=7\)
⑨\(=\sqrt{121}=11\)
⑩\(=-\sqrt{36}=-6\)
⑪\( \displaystyle \sqrt{\frac{1}{4}} \)
⑫\( \displaystyle \sqrt{\frac{25}{36}} \)
⑪\(\displaystyle \frac{1}{2} \)
⑫\(\displaystyle \frac{5}{6} \)
根号をはずすのはたくさん数をこなしましょう。とりあえず2乗の数にすれば√根号ははずせるということを覚え、問題をたくさん解きましょう。
(4)平方根の大小
2< 10…中の数が大きいほど大きくなります。
- 2>- 3 の場合は、-2の方が大きいのでこのように表します。
では、根号がついている数字の大小はどうやって判断すればよいでしょうか。
(大小比較)
√15と4はどちらが大きいか。
↓ ↓2乗する!
15<16 A.4
☆ルートの大きさは2乗して比べる!
いったん、√根号をはずして、つまりすべての数を2乗してから、改めて大きさを比べればよいのです。
※学校の先生によって、ルートをはずすのではなく、ルートをつけることによって比べさせる先生もいるようです。
√15と4はどちらが大きいか
↓
√15<√16
問 どちらが大きいか?
① √8と2 ② - √3と- √5
2乗する!
①8>4 ②ー3>ー5
※②については、ーマイナスは2乗せず、数字のみを2乗してみるようにしましょう。