2次関数のグラフの動き、形を見ていきます。
まず、式によってどのように数値が変わるかを図示します。
①\( \displaystyle y=\frac{1}{2}x^2 \)
\begin{array}{c|ccccc}
x & -1 & 0 & 1 & 2 & 3 \\
y & \displaystyle \frac{1}{2} & 0 & \displaystyle \frac{1}{2} & 2 & \displaystyle \frac{9}{2}
\end{array}
②\( \displaystyle y=x^2 \)
\begin{array}{c|ccccc}
x & -1 & 0 & 1 & 2 & 3 \\
y & 1 & 0 & 1 & 4 & 9
\end{array}
③\( \displaystyle y=2x^2 \)
\begin{array}{c|ccccc}
x & -1 & 0 & 1 & 2 & 3 \\
y & 2 & 0 & 2 & 8 & 18
\end{array}
④\( \displaystyle y=-x^2 \)
\begin{array}{c|ccccc}
x & -1 & 0 & 1 & 2 & 3 \\
y & -1 & 0 & -1 & -4 & -9
\end{array}
ここから、点を取って線を引いていくと、図のようになります。
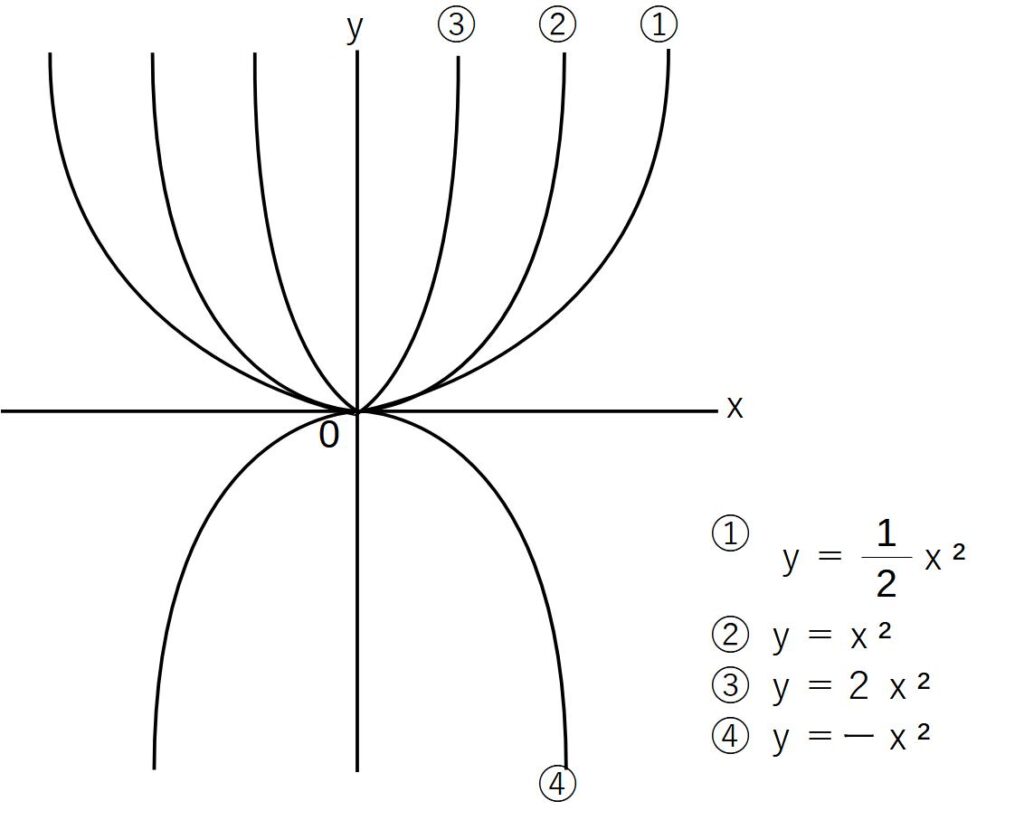
2次関数のグラフの特徴
①原点を通る放物線である
②y軸に対して対称になる
③a>0→下にとつの形になる→原点でyが最小
a<0→上にとつの形になる→原点でy最大
④aの絶対値が大きい→開き方が小さくなる