2次関数の変化の割合について勉強します。
その前に、今までの関数の変化の割合について復習します。
例)y=2x+3でxが-1~3まで増加するときの変化の割合
後- 前 変化の割合
y=1 → 9 9- 1 8
x =-1 → 3 変・割=3-(-1)=4
yの変化量/xの変化量=2
※変化の割合は一定
この方法で変化の割合を求めました。
では、2次関数で同じ方法でやってみましょう。
① y=x2でxが2~4まで増加するとき
y 4 → 16 16-4 12
x 2 → 4 変割=4-2=2
変化の割合=12/2=6…ではない!
② y=x2でxが4~6まで増加するとき
y 16 → 36 36-16 20
x 4 → 6 変割=6-4=2
変化の割合=20/2=10…ではない!
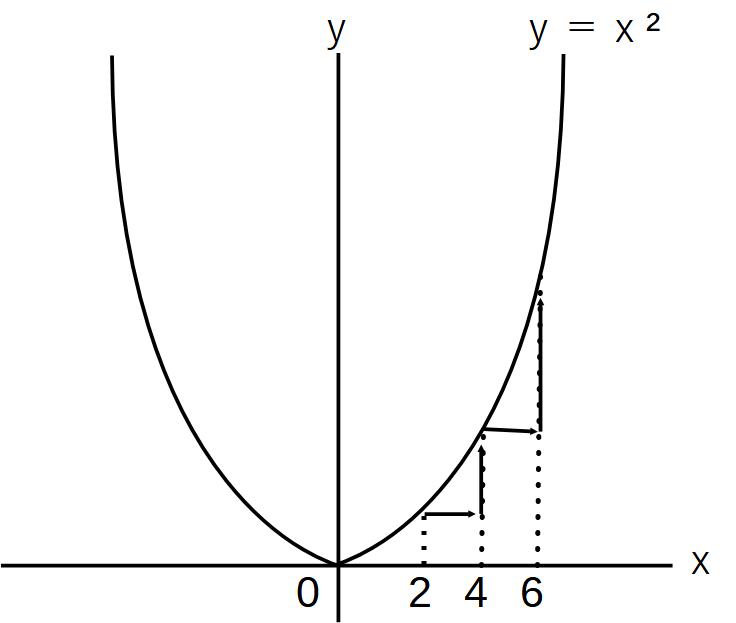
2次関数の変化の割合…2点を結んだ直線の傾き
→とる点によって変わる!
※y=ax2でxがp~qまで増加するとき
変化の割合 a(p+q)
となる
y=2x2のxが次のように変わるときの変化の割合
①1~3 ②2~5 ③-4~-1
2×(1+3) 2×(2+5) 2×(-4+-1)
=8 =14 =-10