2次関数と直線の交点を求める問題の解法を勉強します。
その前に、いままでやってきた直線同士の交点の求め方を復習します。
1次関数のグラフの交点
点Aの座標
y=ax
y=bx+c
この2つの式の連立方程式
代入法でax=bx+cを解いていけば、出せる!
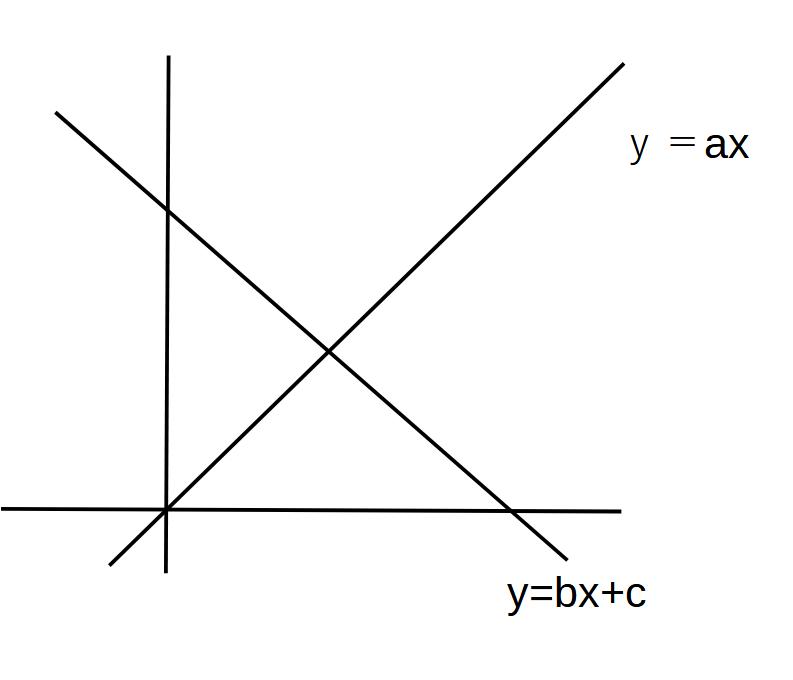
1次関数と2次関数のグラフの交点
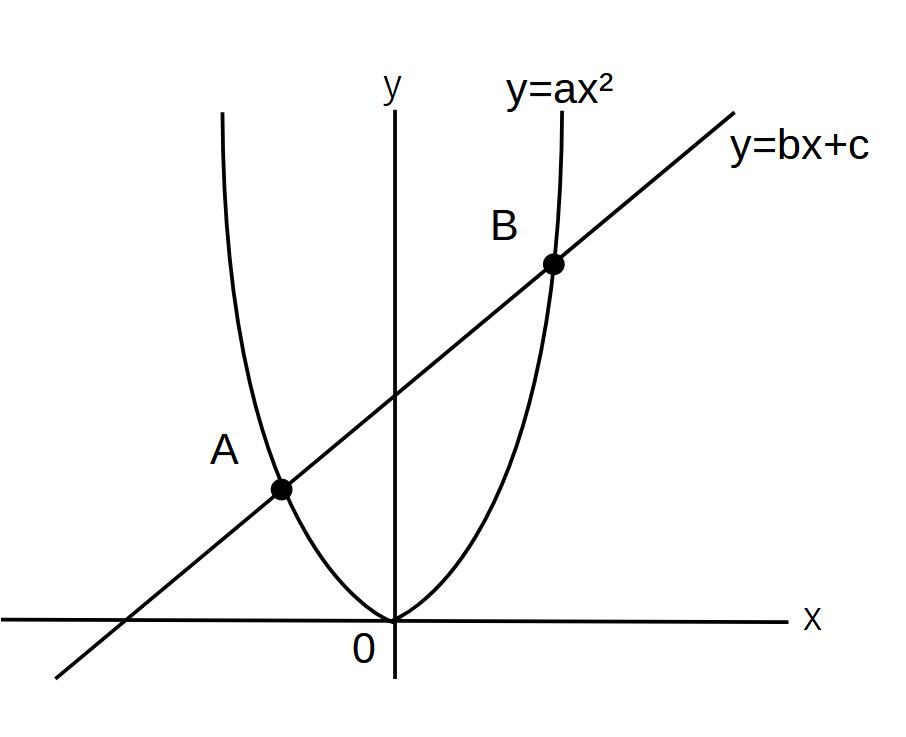
点A、点Bの座標
y=ax²
y=bx+c
この2つの連立方程式を解く!
代入法でax²=bx+c
ax²-bx-c=0 を解く
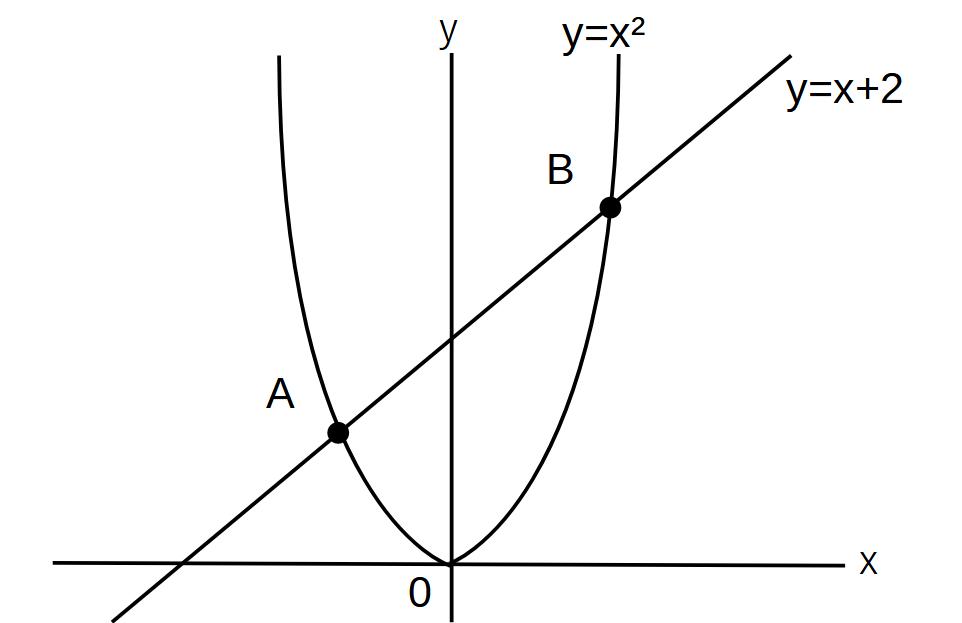
問)
点A、点Bの座標を求めよ。
解)
y=x²
y=x+2 の連立方程式を解く
x2=x+2
x2-x-2=0
(x+1)(x-2)=0 x=-1、2
x=-1のときy=1、x=2のときy=4
A(-1,1) B(2,4)

※点の座標を書き込んで確認する、代入してxとyを出す、ということを忘れないように!
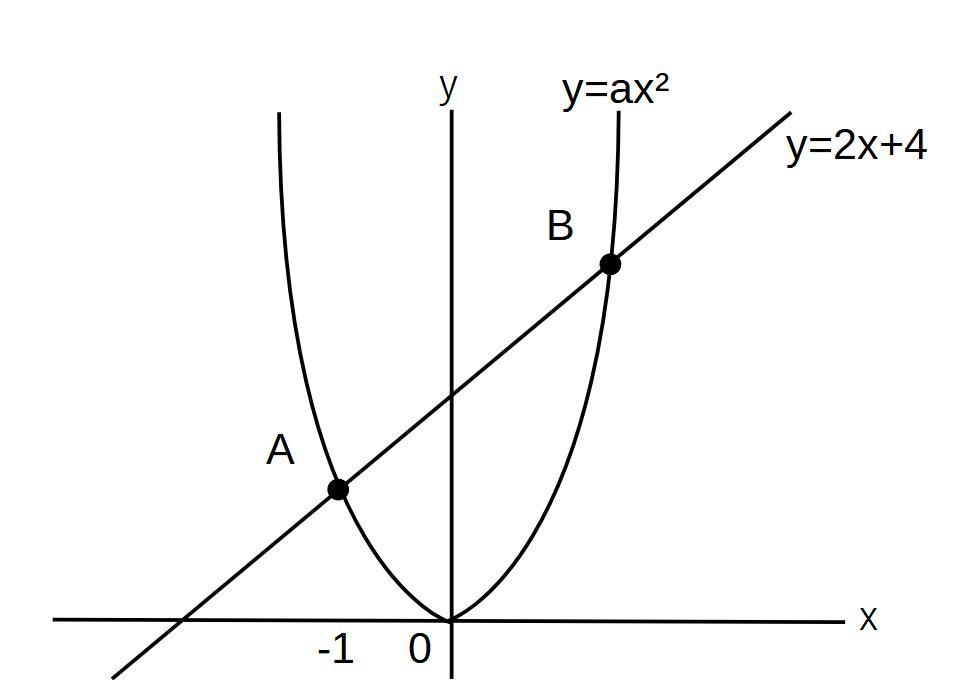
問)
(1)点Aの座標を求めよ。
(2)aの値を求めよ。
(3)点Bの座標を求めよ。
※今回は2次関数のグラフの係数がわからない代わりに、x軸が1つ判明しています。
解)
※手順
わかっている式にわかっている座標を代入
→もう一方の座標がわかる!
→xとyと両方の数値がわかる
→2次関数の式へ代入して係数を求める
(1)x=-1をy=2x+4に代入
y=-2+4
y=2 A(-1,2)
(2)A(-1,2)をy=ax2に代入
2=a(-1)2 a=2
(3)y=2x2とy=2x+4の交点
2x2=2x+4
2x2-2x-4=0
x2-x-2=0
(x+1)(x-2)=0
x=-1、2 ←ー1がA、2がBのx座標
x=2をy=2x2に代入
y=8
B(2,8)