2次関数と1次関数を使った三角形の面積の求め方です。
どこに底辺を置くかを考えながら見ていきましょう。
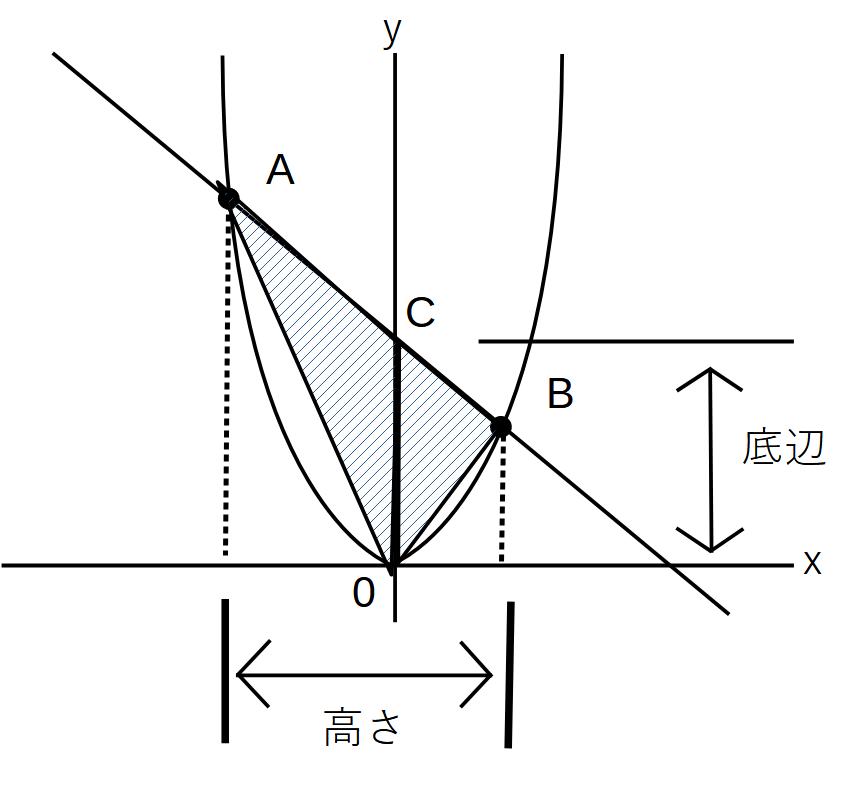
①軸を含む⇒軸を底辺にとる!
△AOBの面積
→底辺OCとしてAのx~Bのxを高さにとる。
(Bのx)-(Aのx)で計算!!
\( \displaystyle △AOB=OC \times (Bのx-Aのx) \times \frac{1}{2} \)
底辺をOCとするのは、2年生でもやりましたが、グラフに関連するところに三角形の底辺を取るときは、x軸またはy軸に平行な直線でとるようにしています。なぜなら高さは等積変形で動かすことができるのに対し、底辺は変形できないので、安定した部分で底辺を取る必要があるからです。
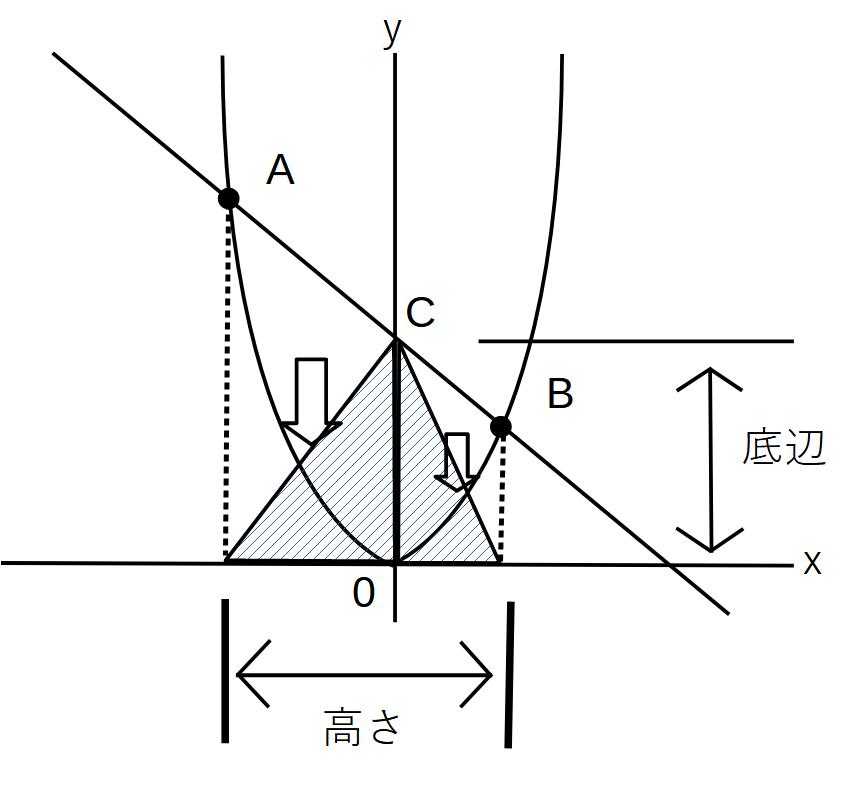
等積変形を行った図です。
斜線部が移動していますが、底辺と高さに変わりがない(この場合は底辺と高さを入れ替えた方がわかりやすいかもですが)ので、形が変わっていても、面積は同じであることがわかります。
今までやってきた知識をすべて集約して解いていく感じになっています。
面積は3つの頂点が出せればでるので、3つの頂点を出すために
①直線の式を求める
②交点を求める
という流れをとります。
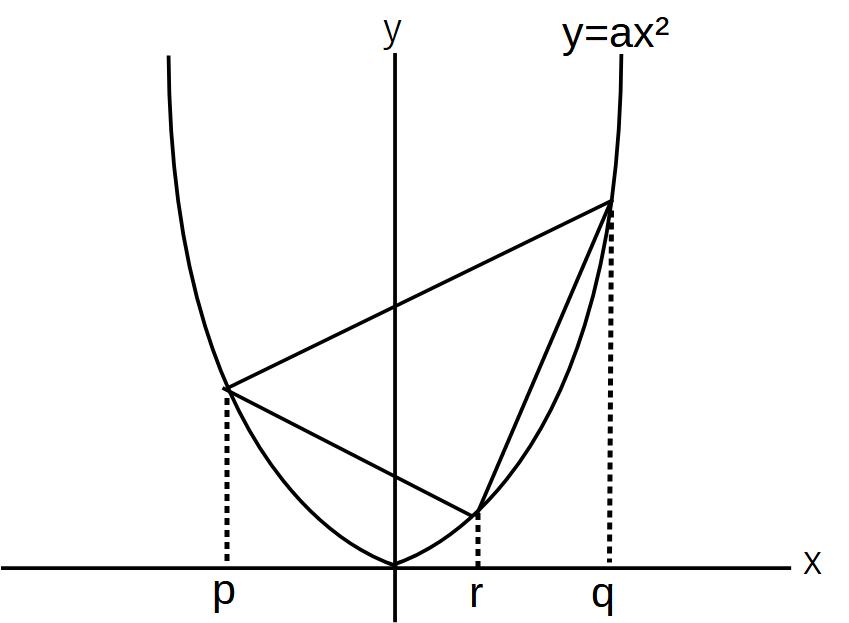
ちなみに、図のような場合の面積をSとすると、
2a(q-r)(r-p)(q-p)
で求められる!
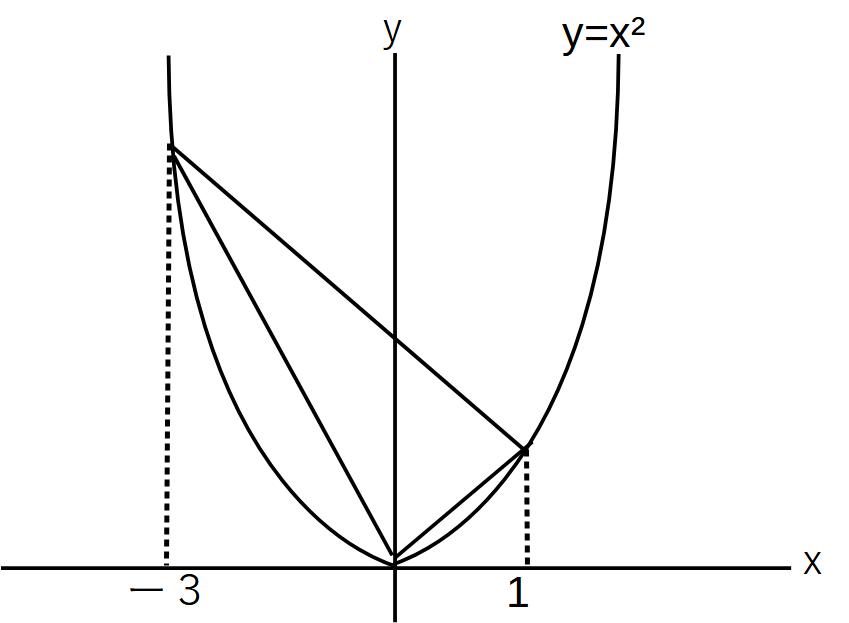
問)
y=x2上にA、Bがある。
(1)A、Bの座標を求めよ。
(2)A、Bを通る直線を求めよ。
(3)△AOBの面積を求めよ。
解)※x座標を代入してyを求める。
(1) A:y=(-3)2
=9 A(-3,9)
B:y=(1)2
=1 B(1,1)
(2)A、Bを通る直線を求めよ。
y=a(p+q)x-apq
y=1(-3+1)x-1×(-3)×1
=-2x+3
(3)△AOBの面積
※座標は(1)で出ている!
底辺DO=3
高さA~B=4
△AOB=1/2×3×4=6