今回はパラメータの問題の解法です。
例1)
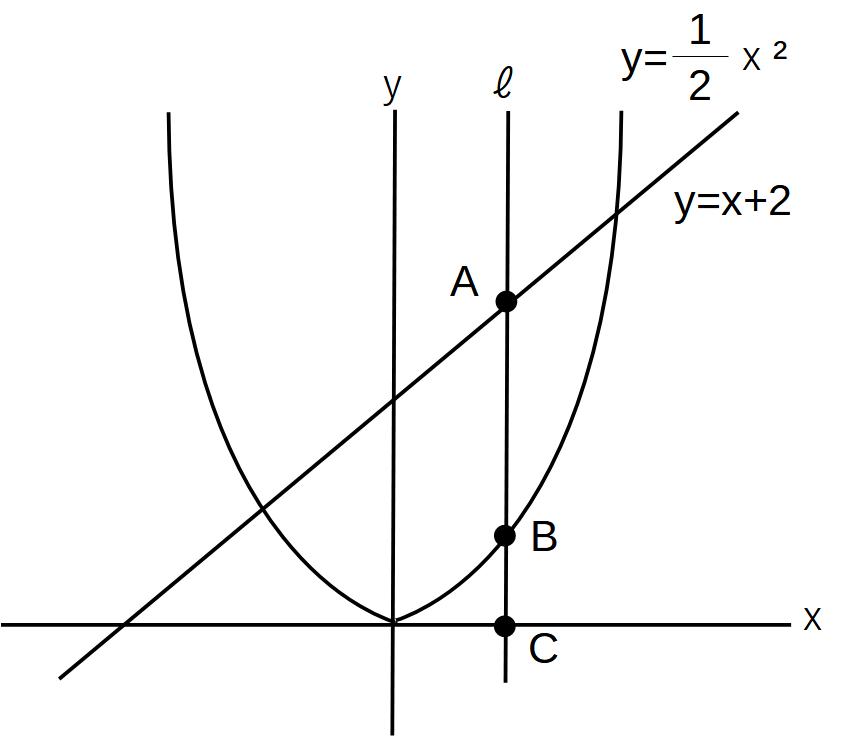
図のようにy=1/2x²の放物線と直線y=x+2があり、さらにy軸に平行な直線x=aがあり、y=1/2x²の放物線と直線y=x+2との交点を上からそれぞれA、B、Cとする。
(1)Cのx座標をaとするとき、A、Bの座標をaで表せ。
(2)AB、BCの長さをaで表せ。
(3)AB=BCのとき、aの値を求めよ。
(1)Cのx座標をaとするとき、A、Bの座標をaで表せ。
Cのx座標がa→A、Bもx座標はa
※たてに並ぶ点…x同じ
よこに並ぶ点…y同じ
Aはy=x+2上の点
x=aを代入すると
y=a+2
よって、A(a,a+2)
Bはy=1/2x2上の点
x=aを代入すると
y=1/2a2
よって、B(a,1/2a²)
(2)AB、BCの長さをaで表せ。
※たての長さ…yでみる
よこの長さ…xでみる
※長さ=大きい座標-小さい座標
AB=Aのy-Bのy
=a+2-1/2a²
BC=Bのy-Cのy
=1/2a²
(3)AB=BCのとき、aの値を求めよ。
a+2-1/2a2=1/2a2
-a2+a+2=0
a2-a-2=0
(a-2)(a+1)=0
a=2、-1
例2)
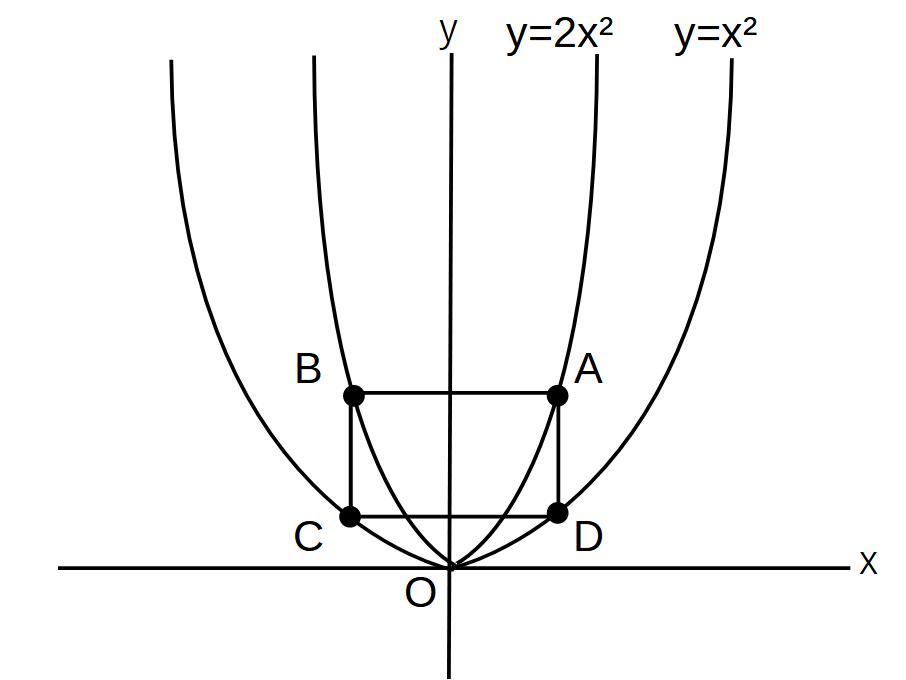
図のようにy=2x²とy=x²の2つの放物線があり、y=2x²上に点A、Bを取り、y=x²上に点C、Dを取り四角形ABCDを作る。
(1)Aのx座標aとするとき、B、C、Dの座標をaで表せ。
(2)ABCDが正方形のとき、Aの座標を求めよ。
(1)Aのx座標aとするとき、B、C、Dの座標をaで表せ。
Aはy=2x2上の点より
(a,2a2)
DはAとxが同じ(x=a)
y=x2上の点より
(a,a2)
※BCについては、2次関数のy軸が同じ点は、y軸について対称になる!
BはAの対称点なので
(-a,2a2)
CはDの対称点なので
(-a,a2)
(2)ABCDが正方形のとき、Aの座標を求めよ。
正方形…たて、よこの長さ同じ!
たて(AD):Aのy-Dのy
2a2-a2
=a2
よこ(AB):Aのx-Bのx
a-(-a)
=2a
たて=よこ
a2=2a
a2-2a=0
a(a-2)=0
a=0、2
長さ0は×
a=2 A(2,8)