(1)ピラミッド形
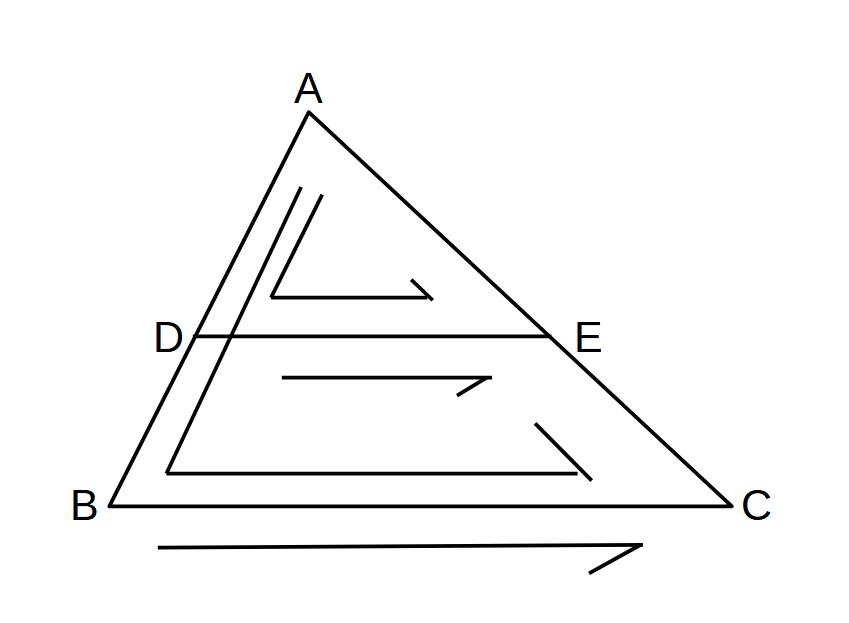
BC//DEのとき
△ABC∽△ADE
対応する辺
AB:AD=AC:AE=BC:DE
(2)ちょうちょ形
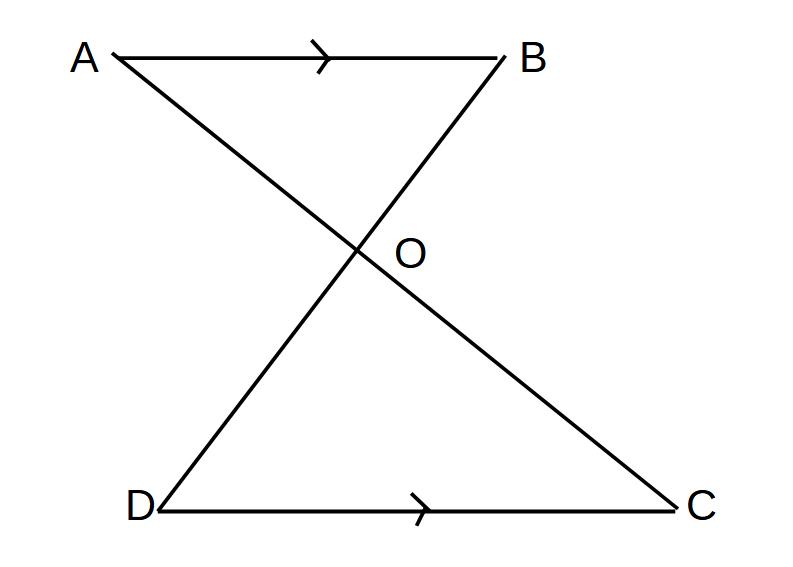
AB//DCのとき
△AOB∽△COD
対応する辺
AO:CO=BO:DO=AB:CD
例1)
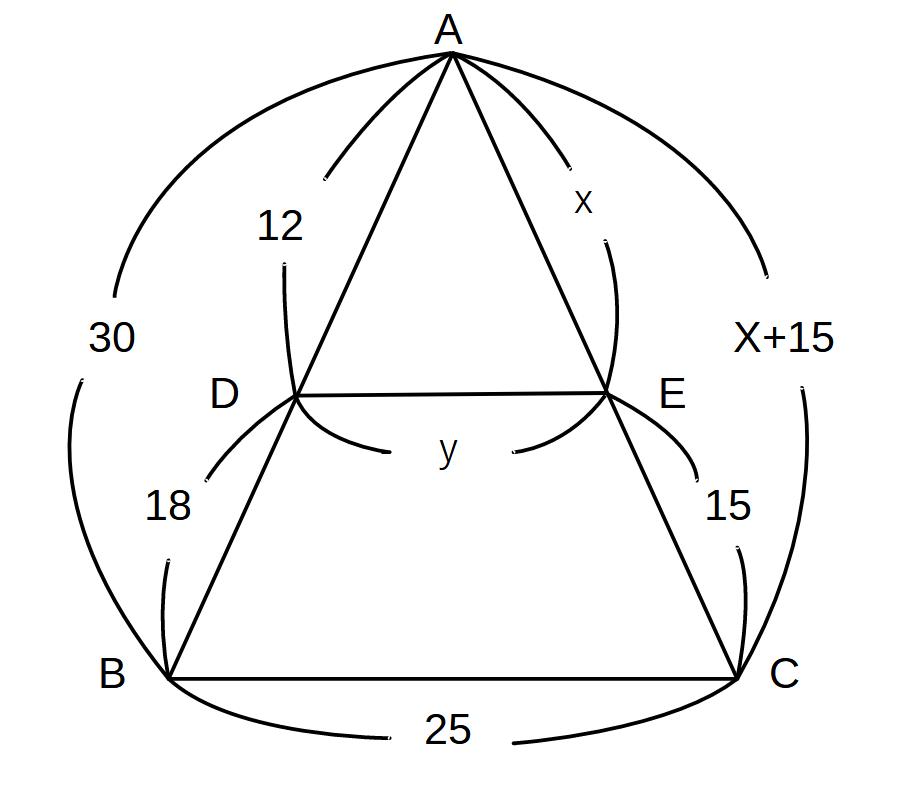
12:30=y:25
5y=50
y=10
x:x+15=2:5
2(x+15)=5x
2x+30=5x
3x=30
x=10
※ここで注意!
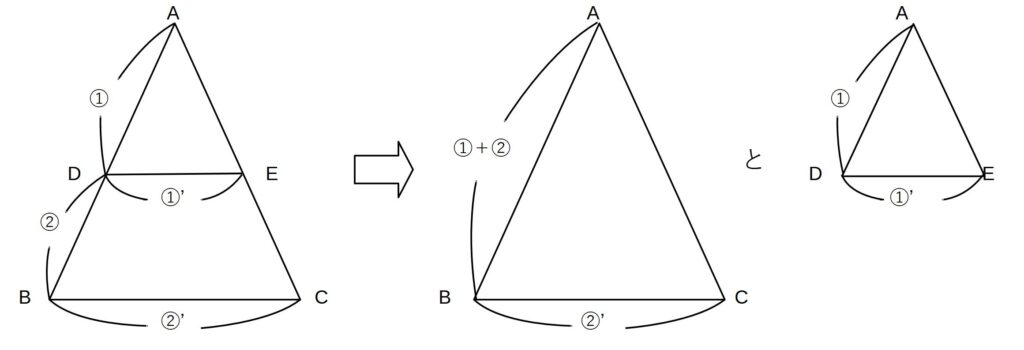
問題では、比を取るときに、
DE:BC=AD:AB
ととるようにするのですが、よくやる間違いで、
DE:BC=AD:DB
ととってしまう人が結構います。
三角形の斜辺同士の比であれば、このような取り方をしますが、底辺との関係ではその取り方をしてはいけません。
考え方として、図のように、比を2つの三角形としてみれば、大きい方の三角形の辺(ここではAB)と、小さい方の三角形の辺(AD)とが対応していることがわかります。
相似では、きれいに図形が並んでいるとは限りません。
むしろ、重なっていたり接していたりするなどして、一見、相似であることがわかりにくくしてあることが大半です。
惑わされないよう、どの三角形のどの部分が相似の条件にあるのかを判断できるようにしましょう。
例2)
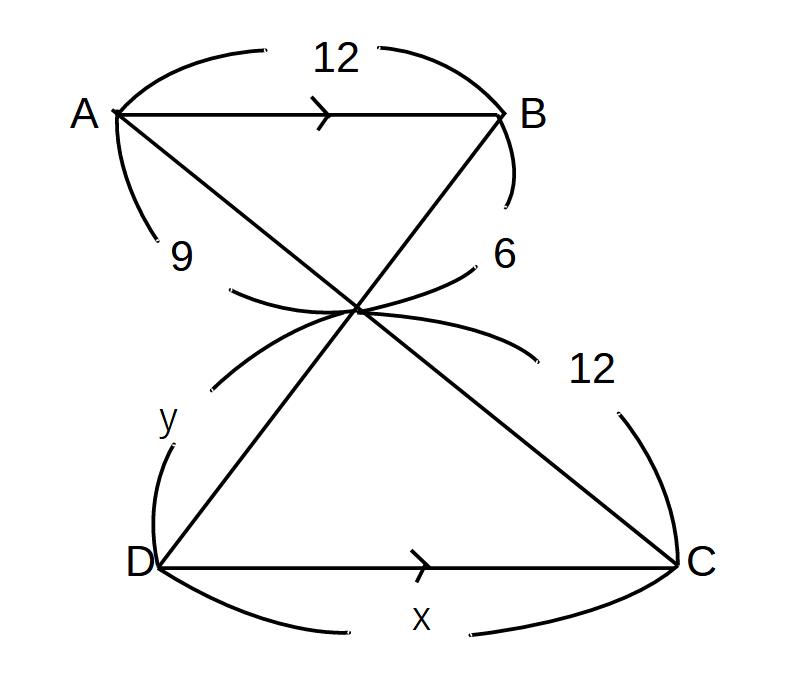
9:12=12:x
3x=48
x=16
3:4=6:y
3y=24
y=8
この例1と例2の問題では、相似の関係にある2つの図形が重なる、接するなどして、新たな図形を作り、その中から相似な図形を見つけ出して、その比を割り出し、計算する、といったものです。
正直言って、図がややこしくなればなるほど、途中から何をやっているのか混乱してしまう可能性が高いです。
ですので、比はちゃんと図形に矢印などを打ち、それで相似の関係を整理するようにしましょう。
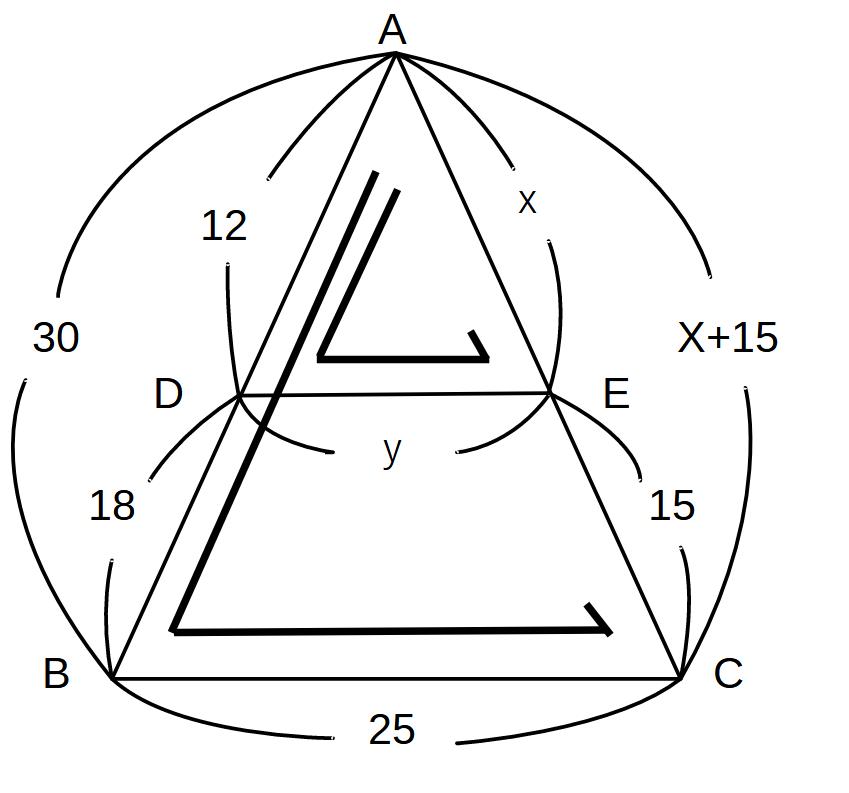
例1)の場合
相似を見つけて、対応する部分に矢印を引く
矢印の形の通りに式を立てる
12:y=30:25
12:y=6:5
6y=60
y=10
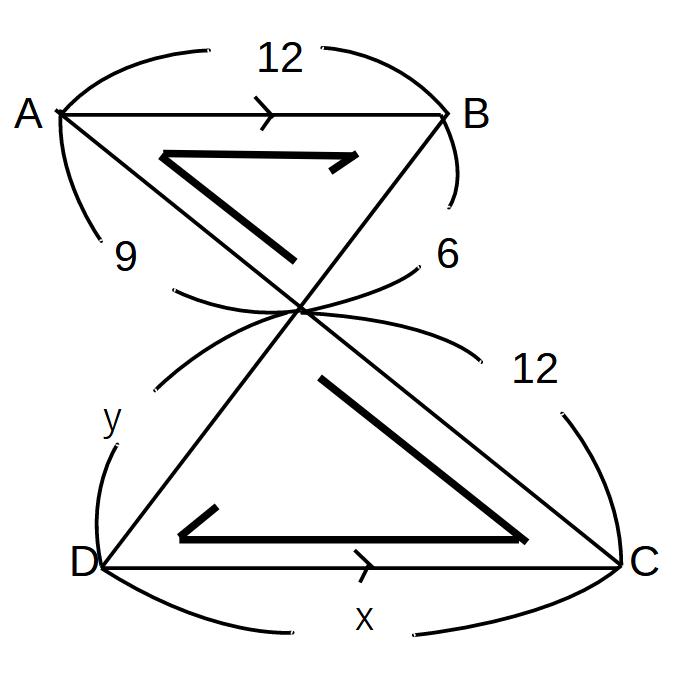
例2)の場合
相似を見つけて、対応する部分に矢印を引く
矢印の通りに式を立てる
9:12=12:x
3x=48
x=16