今回は相似の問題の中でも、基礎的かつ典型的な問題に触れていきます。
いろいろな形があるが、パターンはほぼ決まっています。
1つずつ解き方を定着させていってください。
入試になると、自分で判断する力が要求されるので、その前準備だと思って、しっかりやり方を覚えて、演習を反復するようにしましょう
。
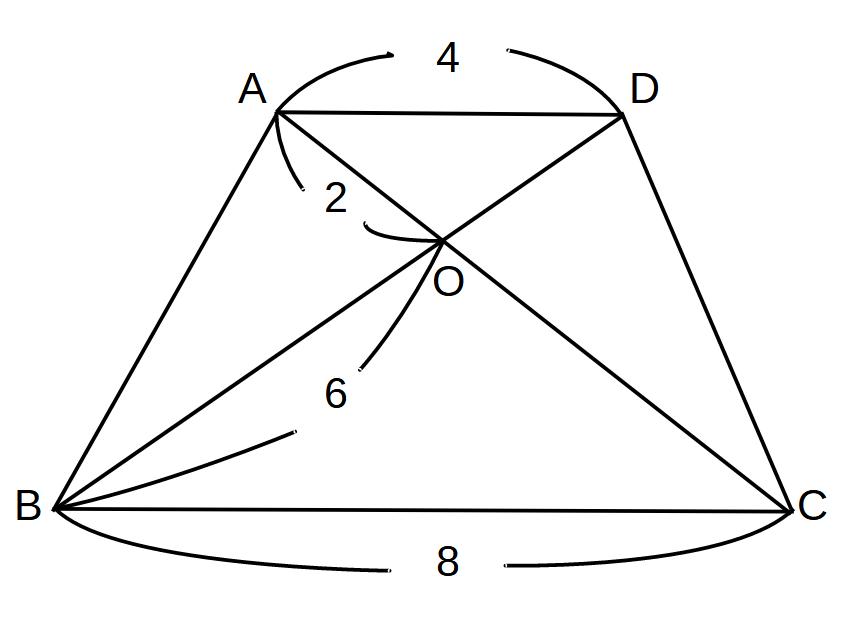
①
AD//BCのとき、
(1)AO:CO
(2)COの長さ
(3)DOの長さ
をそれぞれ求めよ。
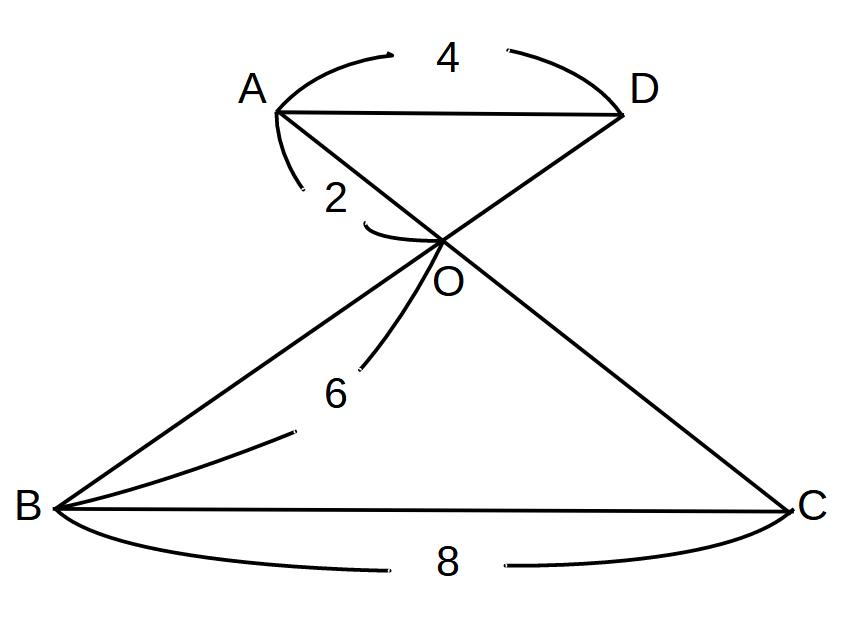
解)
まず、ピラミッド・ちょうちょを見つける!
相似比は4:8=1:2
(1)AO:CO=1:2
(対応する辺)
(2)AO:CO=1:2
2 :CO=1:2
CO=4
(3)DO:BO=1:2
DO: 6 =1:2
2DO=6
DO=3
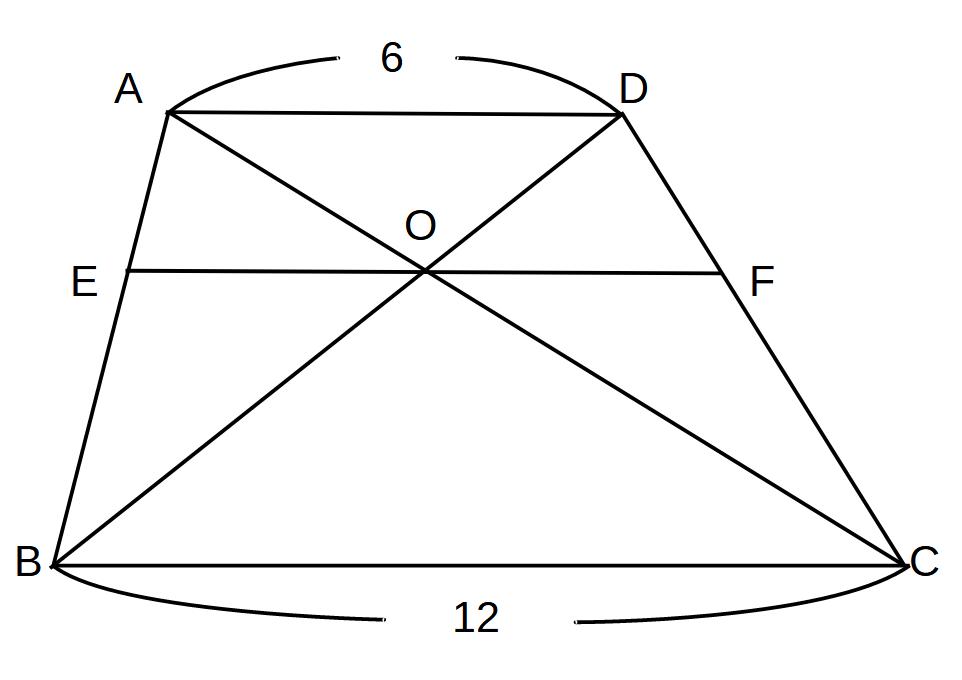
②AD//EF//BCのとき
(1)EO:BC
(2)EFの長さ
をそれぞれ求めよ。
→まずはピラミッド・ちょうちょを見つける!
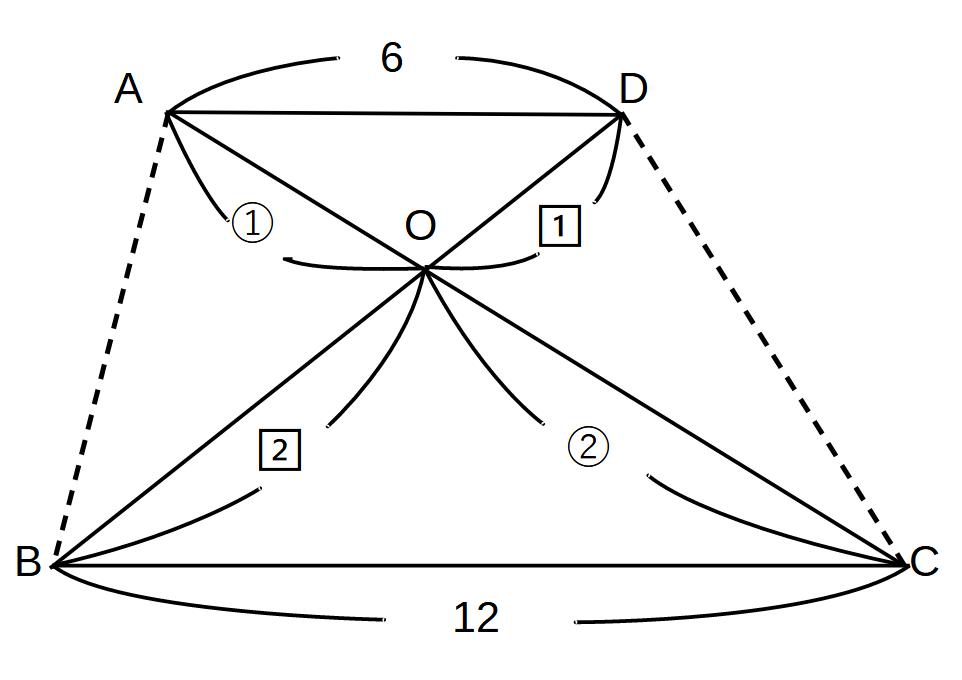
まずちょうちょを見つけて、
△AOD:△COB
= 1 : 2
を発見
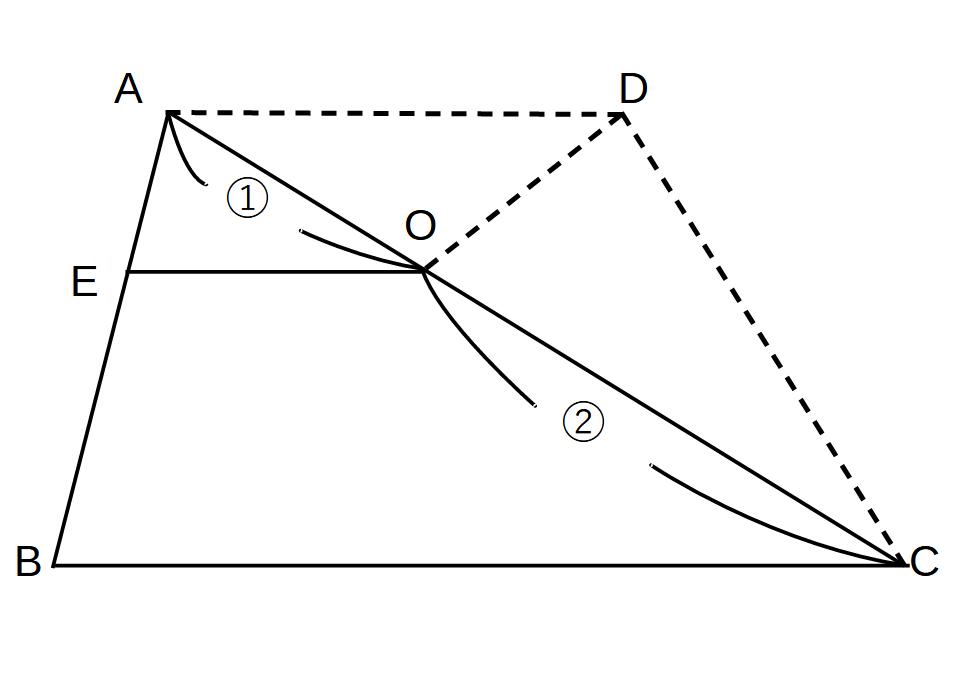
次はピラミッドです。
△AEO:△ABC
= 1 : 3
となります。
ピラミッドは1つではありません。
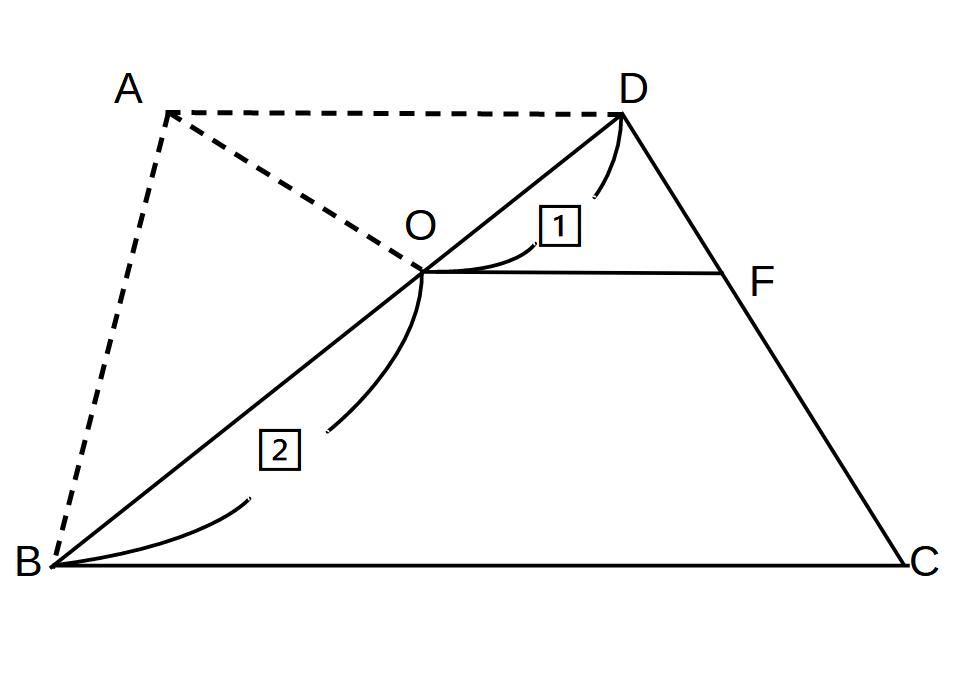
もう1つのピラミッドです。
△DOF:△DBC
= 1 : 3
(1)EO:BC
図2より1:3
(2)EOの長さは、
EO:BC=1:3
EO:12=1:3
EO = 4
FOの長さは、
FO:BC=1:3
FO:12=1:3
FO =4
よってEF=8
図形が入り組んでいる、複合図形の場合の比を見つけるときは、比が複数できたりします。
その時に、どれとどれが対応しているか、しっかり判別しながらやることが必要です。
図のように、比の数字に〇や□の囲みをつけて、分けられるようにすれば、間違うことはなくなるはずです。