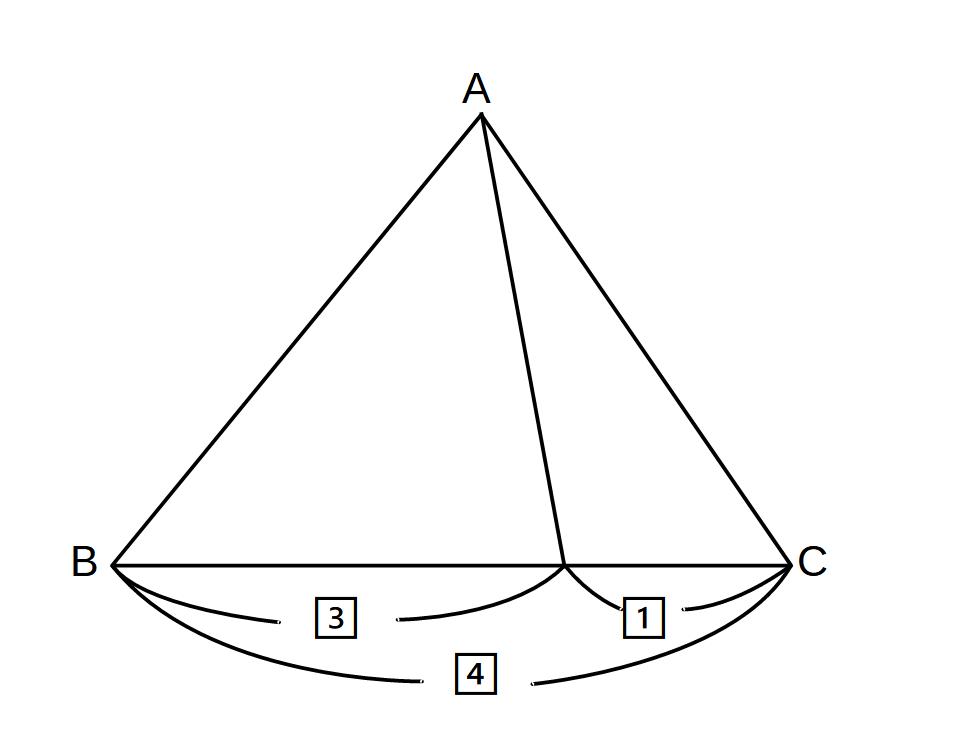
①高さが同じ→底辺の比でみる
△ABD:△ADC= 3 : 1
また、△ABDは△ABC(全体)の3/4
△ADCは 1/4
といえる
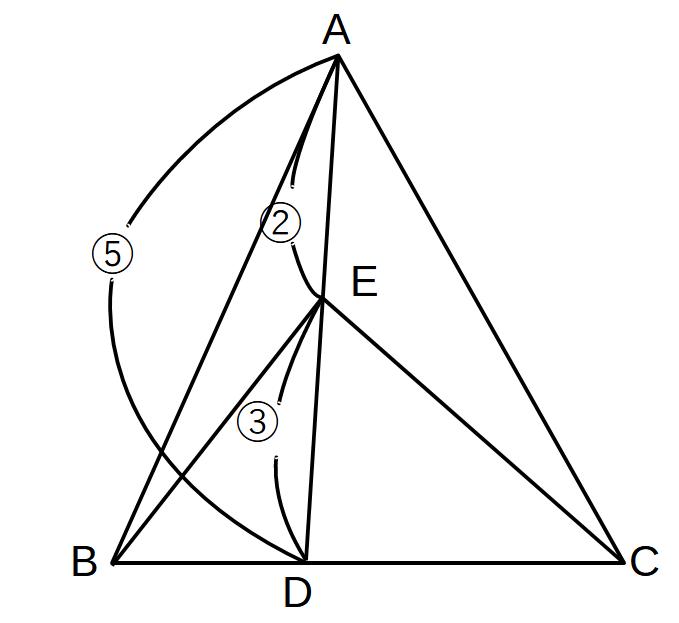
②底辺が同じ→高さの比でみる
△ABC:△BEC= 5 : 3
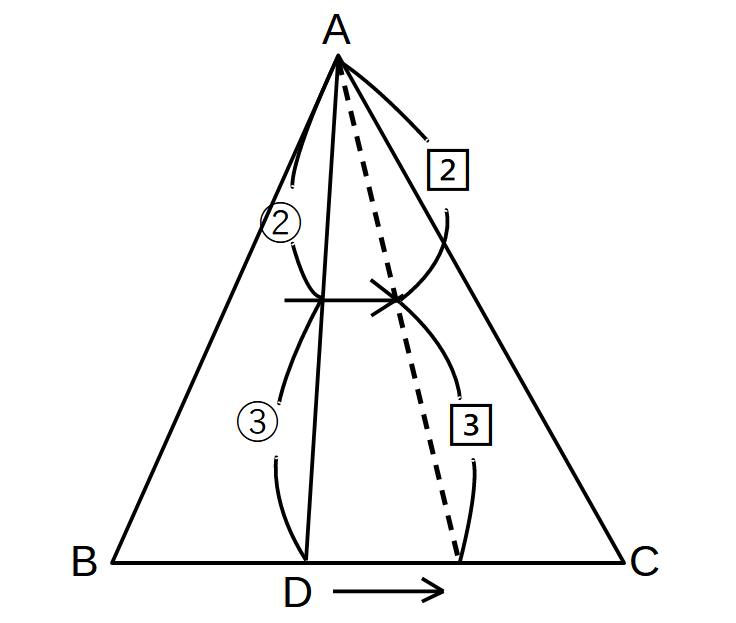
垂直になっていなくても、高さの比と同じになる。
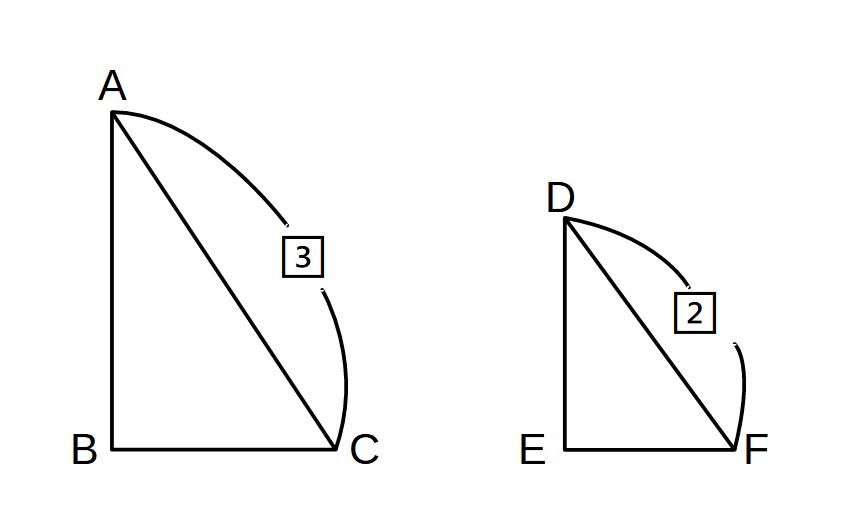
△ABC∽△DEFならば
△ABC:△DEF= 32 : 22
相似な図形では
面積比=(相似比)2
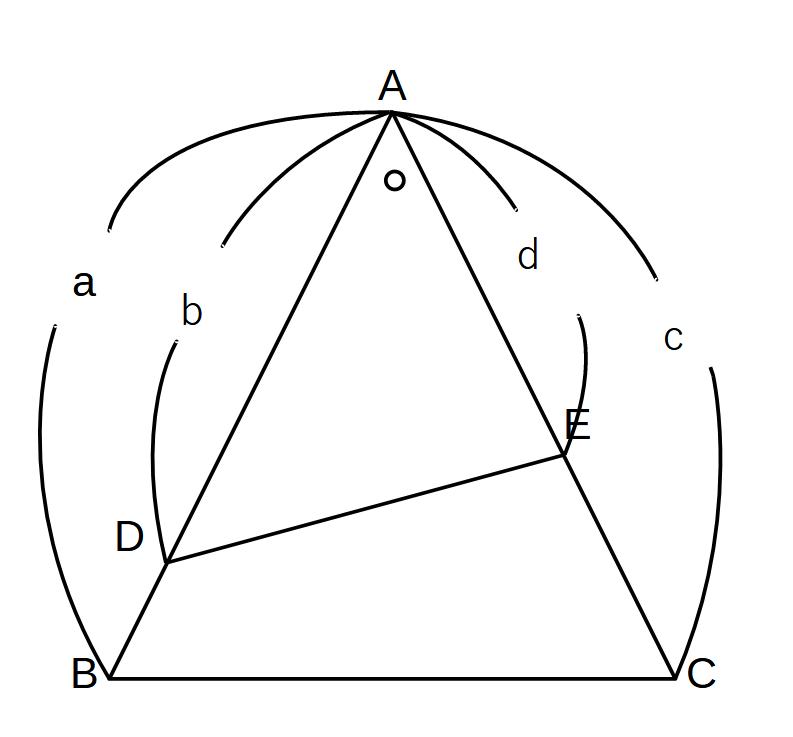
△ADE:△ABC
=a×b:c×d
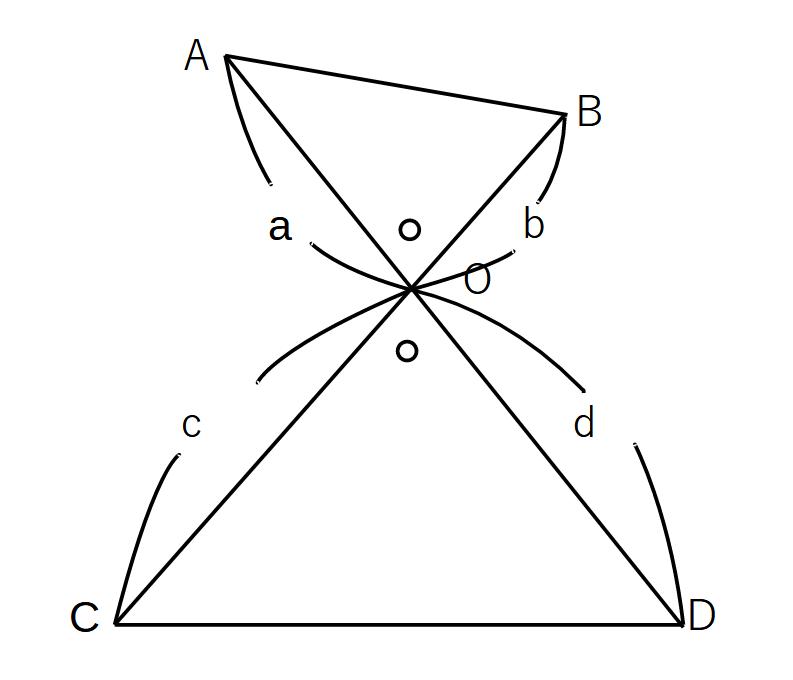
△OAB:△OCD
=a×b:c×d
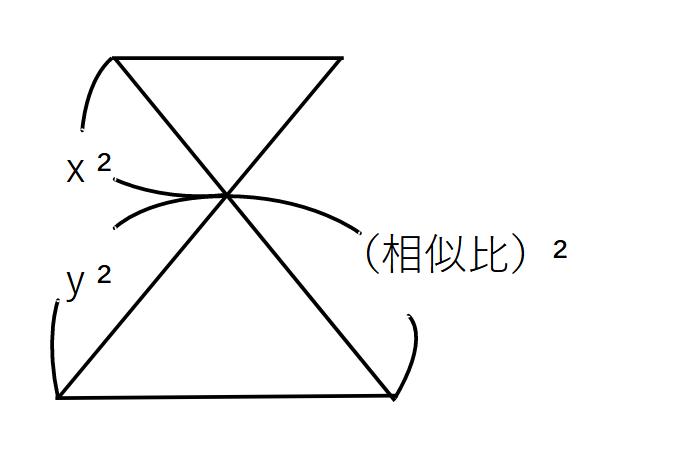
相似形の場合
問1)
ABCDが平行四辺形のとき
(1)△ABP:△APC
(2)△ABP:△ABC
(3)△ABP:△ADC
を求めよ。
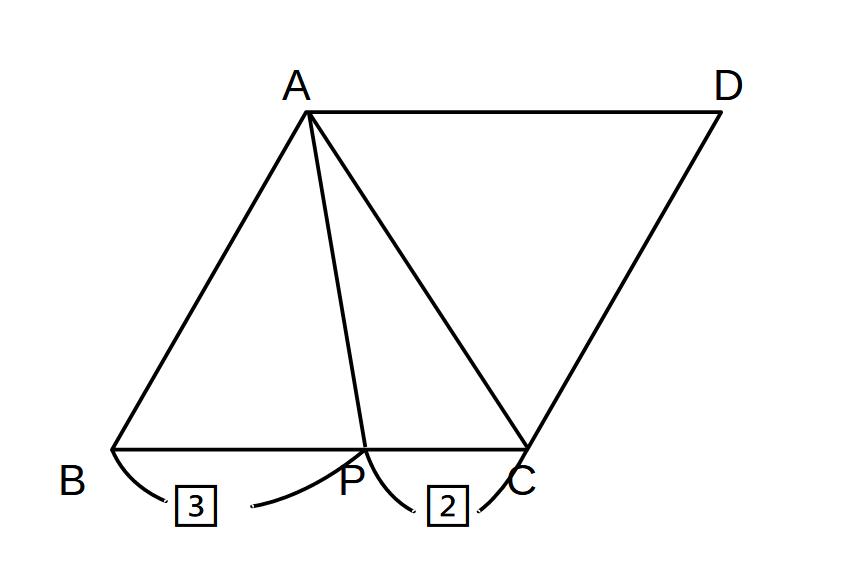
(1)△ABP:△APC
= BP : PC
= 3 : 2
(2)△ABP:△ABC
= BP :BC
= 3 : 5
(3)△ABPと△ADCは高さが等しい
△ABP:△ADC
= BP : AD
= 3 : 5
問2)
(1)△ABC:△EBC
(2)△EBD:△EDC
(3)△AEC:△EDB
を求めよ。
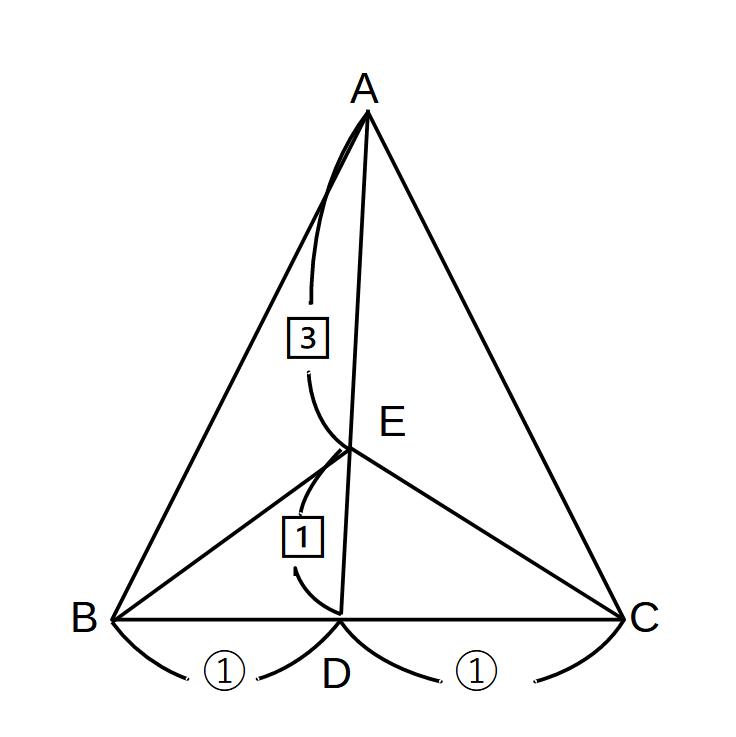
(1)△ABC:△EBC
= AD : ED
= 4 : 1
(2)△EBD:△EDC
= BD : DC
= 1 : 1
(3)△AECと△EDBで
高さの比 BD:DC=1:1
底辺の比 AE:ED=3:1
よって底辺の比から
3 : 1