前回見てきた三平方の定理は、他の比率でも存在します。
(1)三角定規
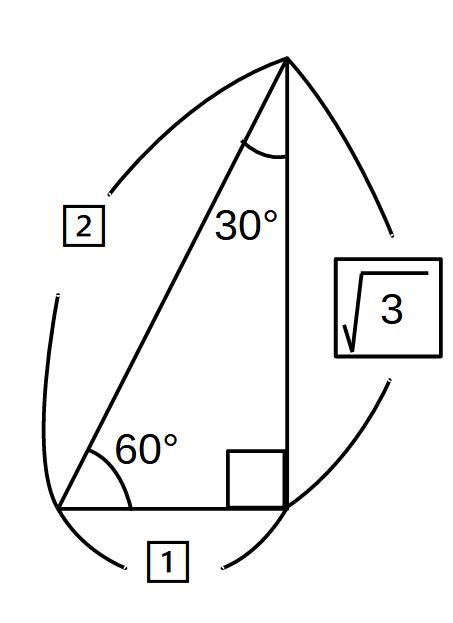
①90°・60°・30°⇒1:2:√ 3
→90°と60°の間が1になります。
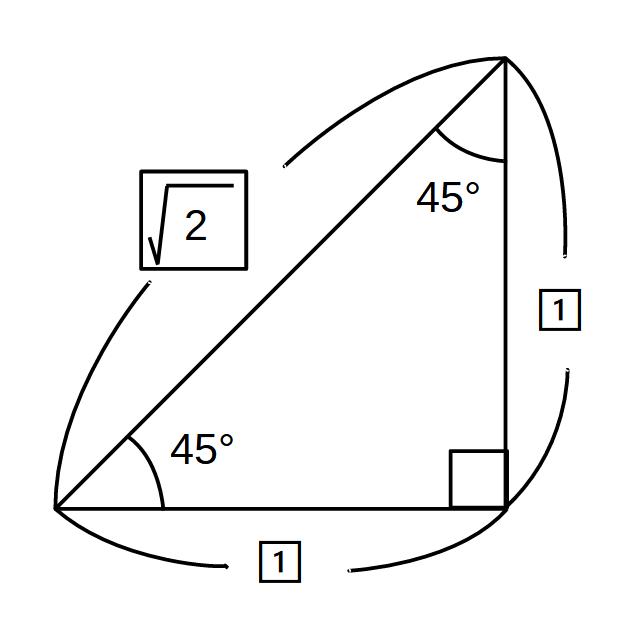
②90°・45°・45°⇒1:1: √2
他にもあります。
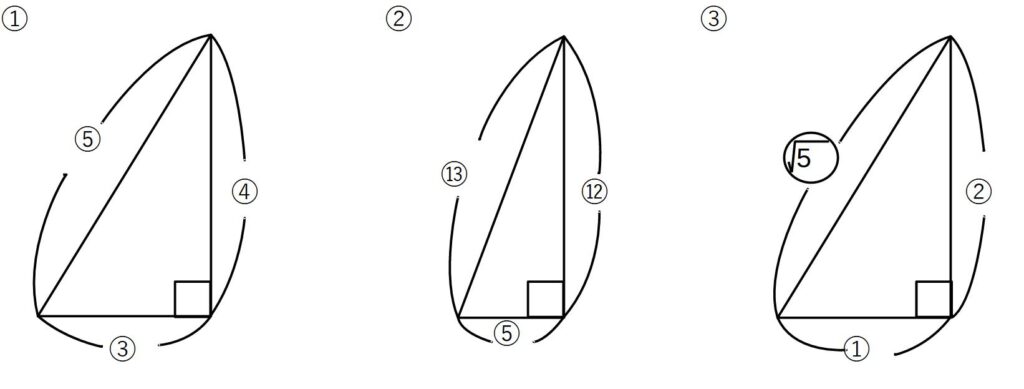
※この3つのうち、③に関しては、先ほどの1:2:√3とかぶっており、混乱してしまう心配がある場合は、③は覚えなくてもよいです。混ざって混乱するよりはマシです。どのみち計算しても出せます。
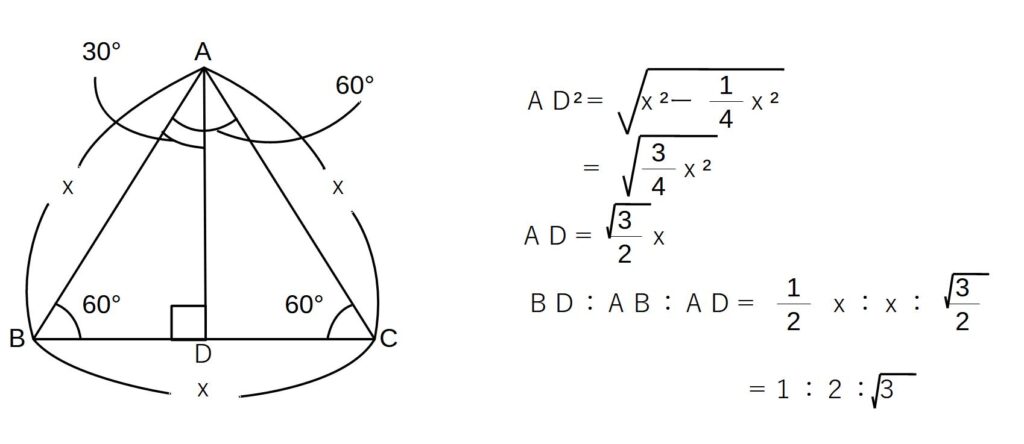
ここで、90°、60°、30°の直角三角形が、正三角形の半分であることの証明をしておきます。
(2)寸法が狂った図
公立高校の入試問題では問題にならないのですが、一部の私立高校の入試問題において、図形について注意しなければならないことがあります。以下の図を見てください。
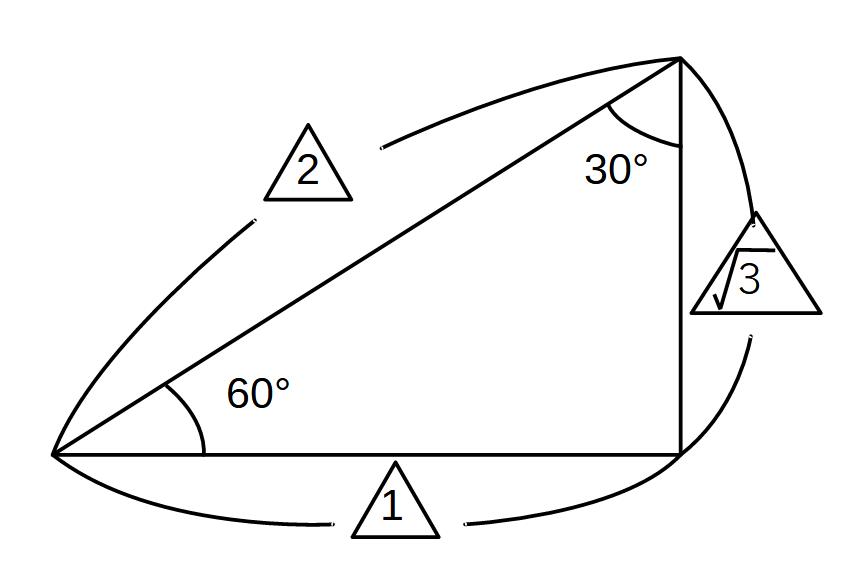
図のようなものが出題されたことがあります。よく見てみると、見た目の角度がおかしいです。30°の角の方が、60°の角より大きく見えますし、実際大きいです。
今までの学校の授業や定期テスト、実力テストでは、このような図はまず出てきません。私立高校の入試で出される可能性があるだけですので、もし、このような図が一部の私立高校の入試で問題として出てきて、その場で初めて対応することになれば、動揺するかもしれませんし、焦って間違った解釈をしたまま解答にかかり、うまく解答できず混乱して時間だけが過ぎていき…ということになりかねません。
こういった場合はあくまで、書いてある角度、数値を頼りに図形を読み取り、解答していきましょう。
実は(1)三角定規の①で、「90°と60°の間が1になります」と書きました。
これは、見た目のおかしい三角形が出題されたとき、効力を発揮します。この「90°と60°の間が1」さえ覚えておけば、あとは図に惑わされることなく比を置くことができ、混乱を避けることができるからです。