(1)面積
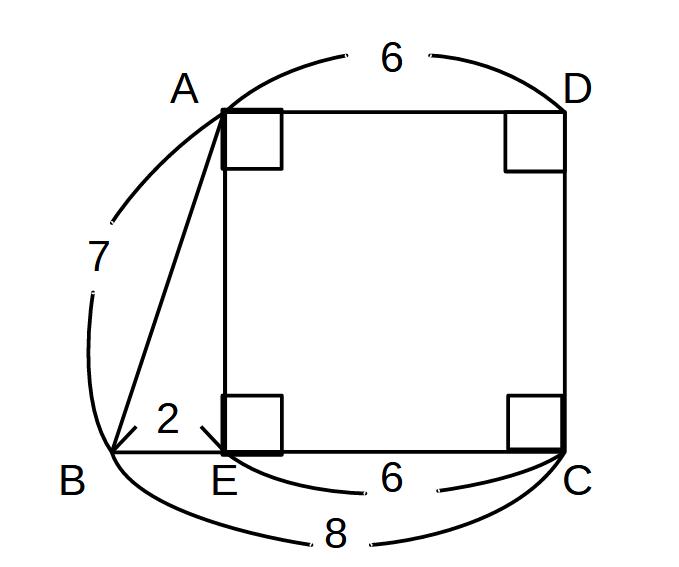
①ABCDの面積を求めよ。
→高さを求めないと出ない!
※直角三角形を作り、高さを求める
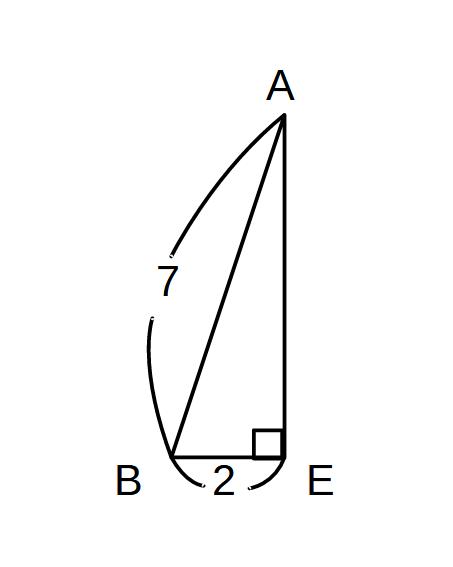
ABEを切り取った図
Aから垂線をおろす
△ABEは直角三角形
AD=ECなので、
BE=2
AB2=AE2+BE2
72=AE2+22
AE2=√345 AE>0
AE=45=3√5
面積=(6+8)×3√5×1/2
=21√5
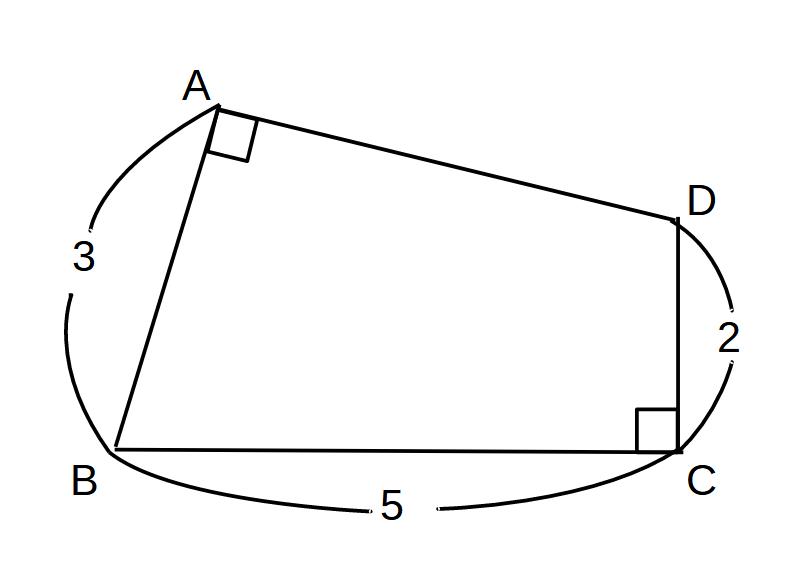
②ABCDの面積を求めよ。
→三角形に分ける
※直角三角形になるように分ける!
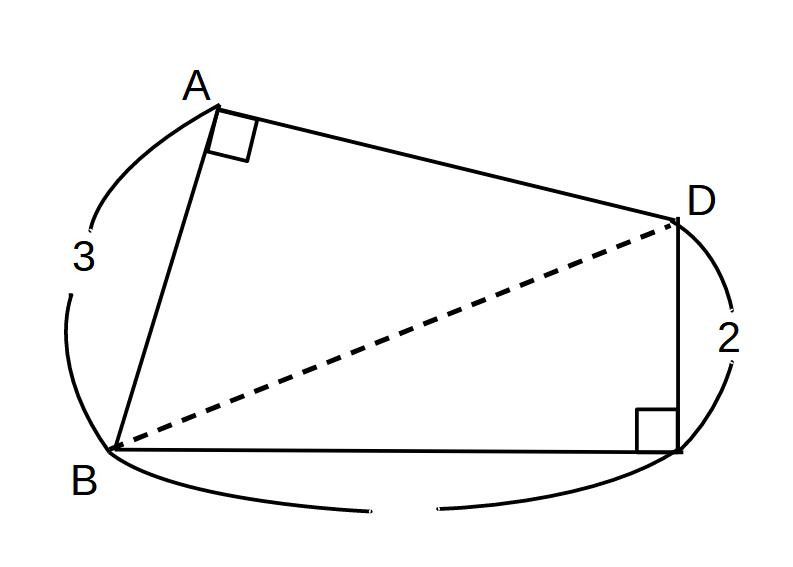
BDをひく。
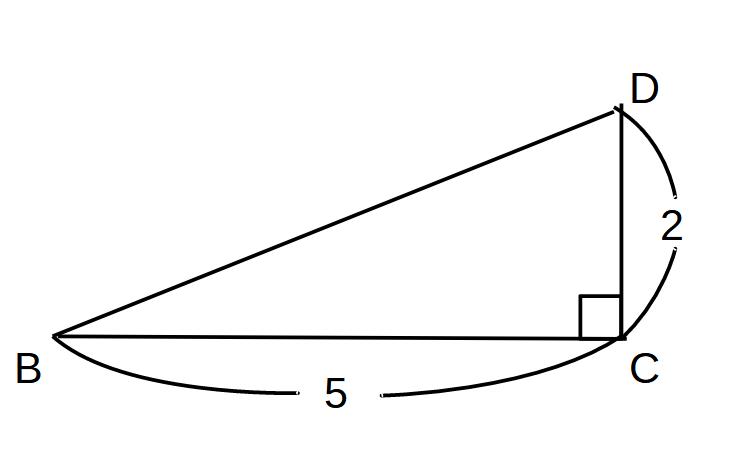

BD2=BC2+DC2
BD2=25+4
BD2=29 BD>0
BD =√29

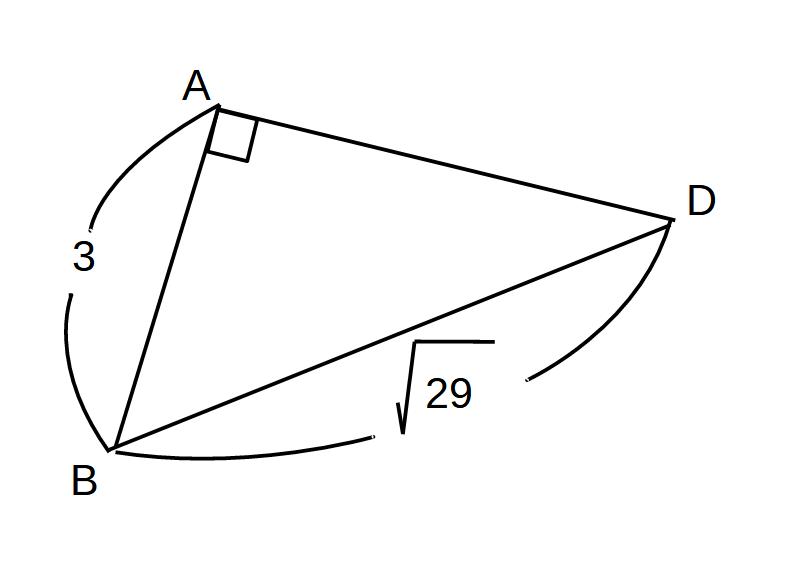
BD2=AB2+AD2
29=9+AD2
AD2=20 AD>0
AD=2√5
2×5×1/2+3×2√5×1/2=5+3√5
△BCD=2×5×1/2=5
△ABD=3×25×1/2=3√5
ABCD=5+3√5
(2)正三角形
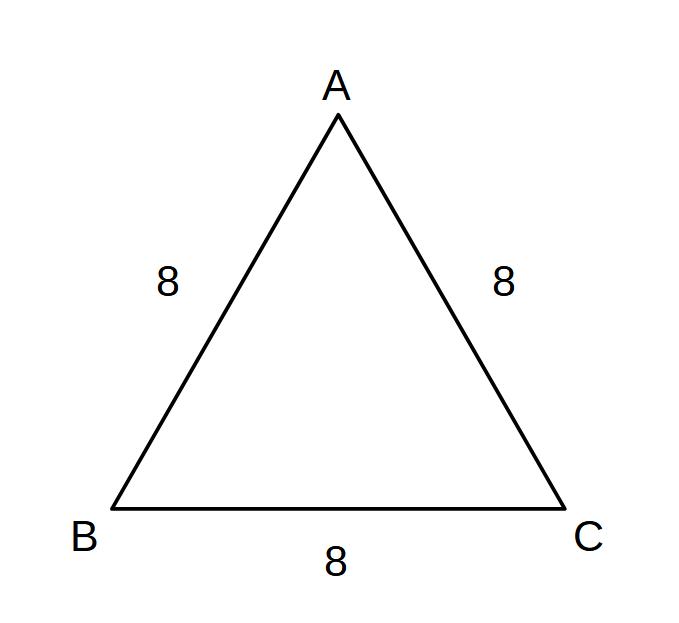
①△ABCの高さ
②△ABCの面積
をそれぞれ求めよ。
正三角、二等辺三角形の高さ(復習)
底辺を垂直に2等分→直角三角形になる!

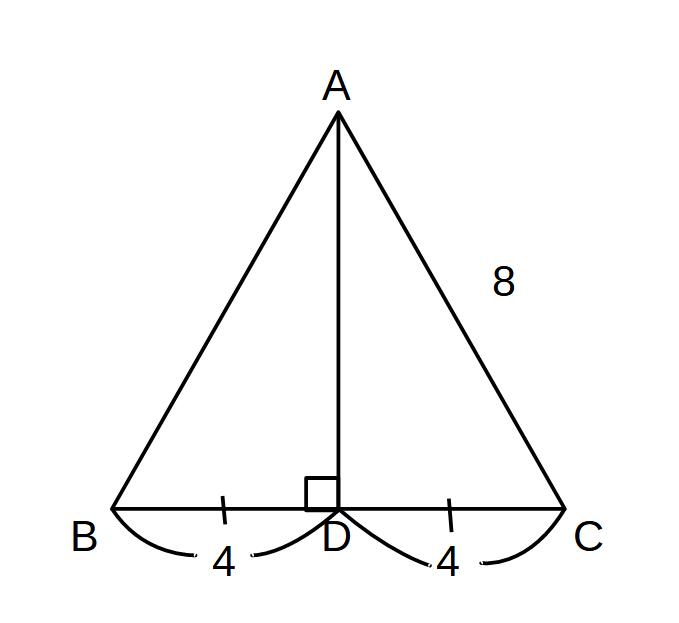
①AC2=AD2+DC2
64=AD2+16
AD>0
AD=√48=4√3
(特別角)
CD:AD=1:√3
4:x=1:√3
x=4√3
②△ABC=8×4√3×1/2
=16√3
(3)等脚台形
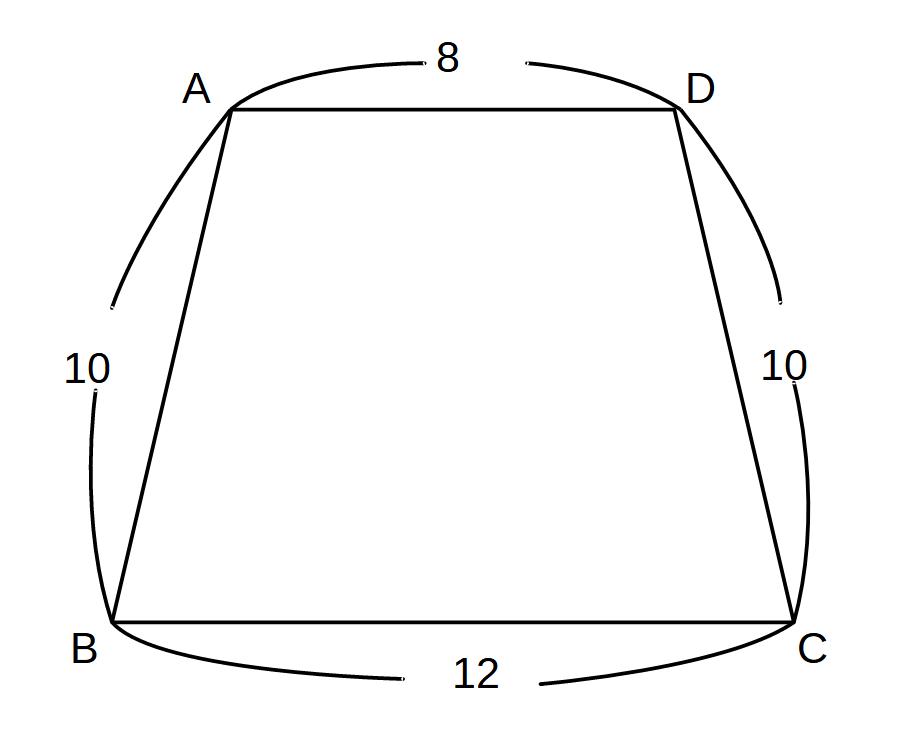
①台形の高さ
②台形の面積
③ACの長さ
をそれぞれ求めよ。
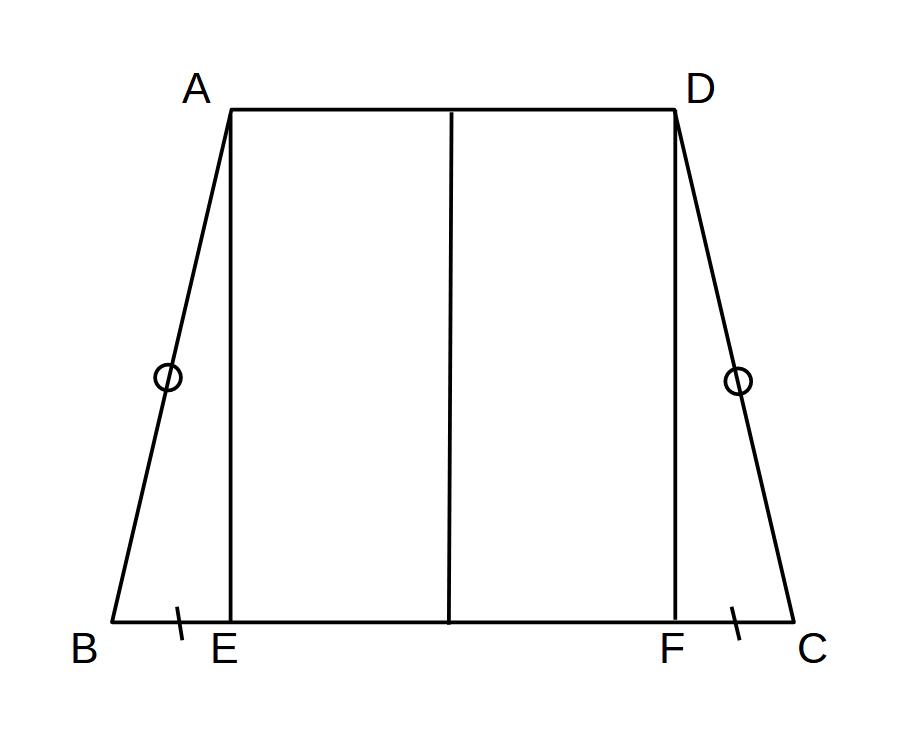
※等脚台形(AB=DC)
BE=FC
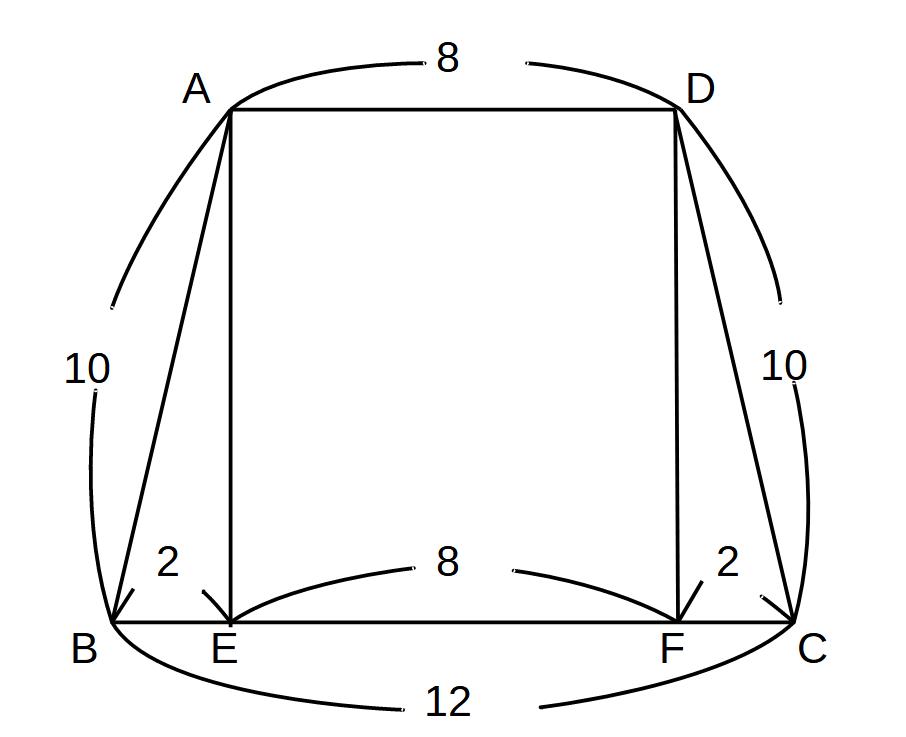
①AB2=AE2+BE2
100=AE2+4
AE2=96 AE>0
AE=√96=4√6
②(8+12)×4√6×1/2=40√6
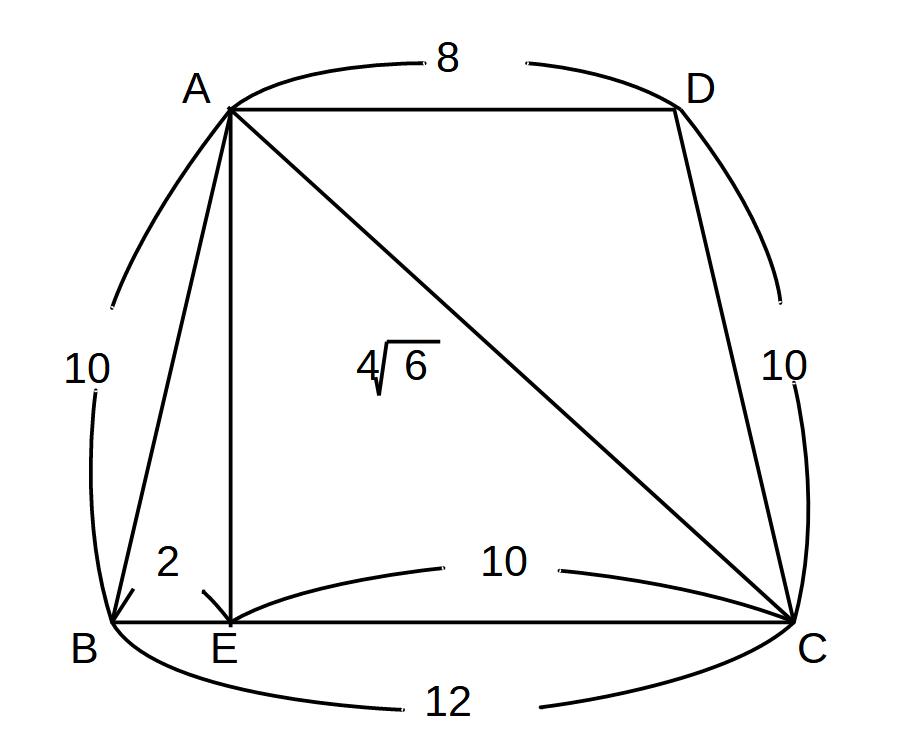
③(1)のAEを使うと直角三角形になる!
AC2=AE2+EC2
AC2=4√62+102
AC2=96+100
AC2=196 AC>0
AC=14
(4)円
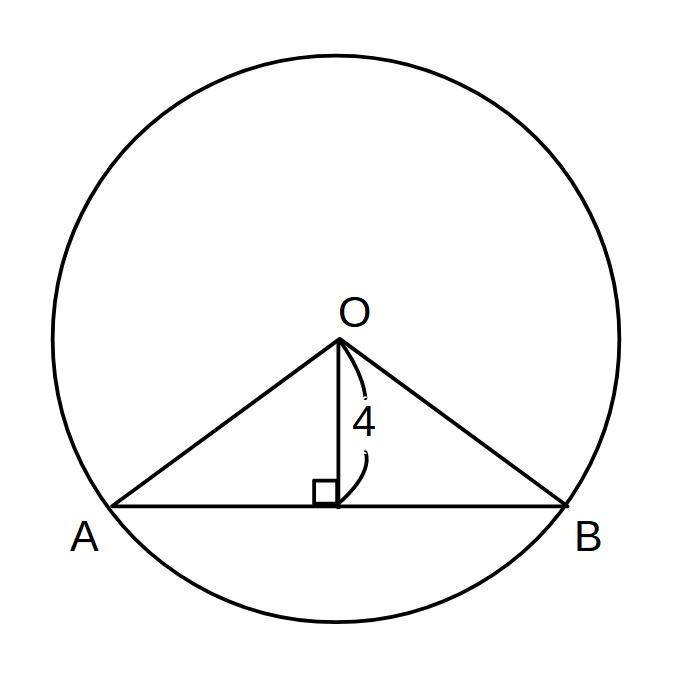
①半径が6の円で、中心から弦ABまでの距離が4のとき、ABの長さを求めよ。
※中心から弦までの距離(=弦におろした垂線)
→弦を垂直に2等分する!
(弦の垂直2等分線は、中心を通る)
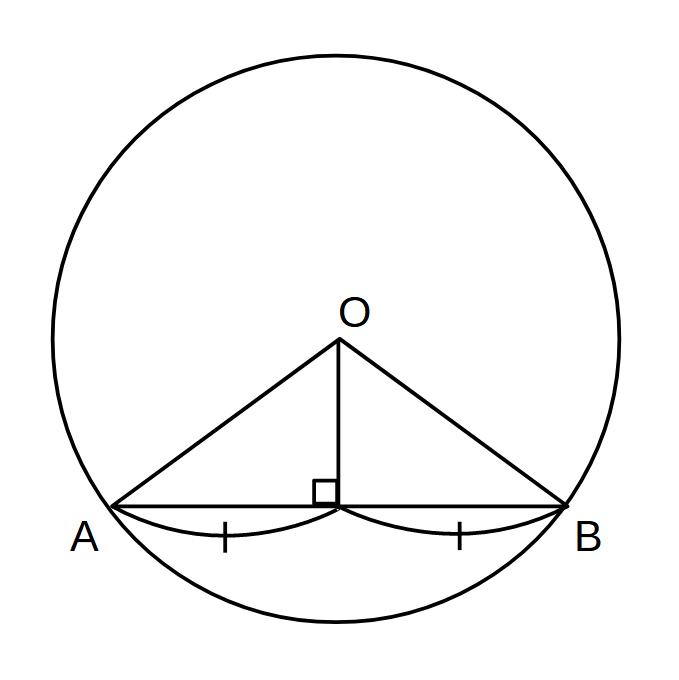
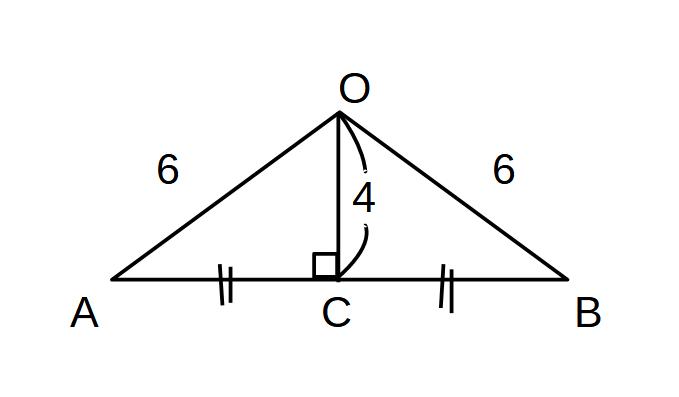
OA=OB=6
OB2=OC2+CB2
36=16+CB2
CB2=20 CB>0
CB=√20=2√5
AB=2CB=4√5
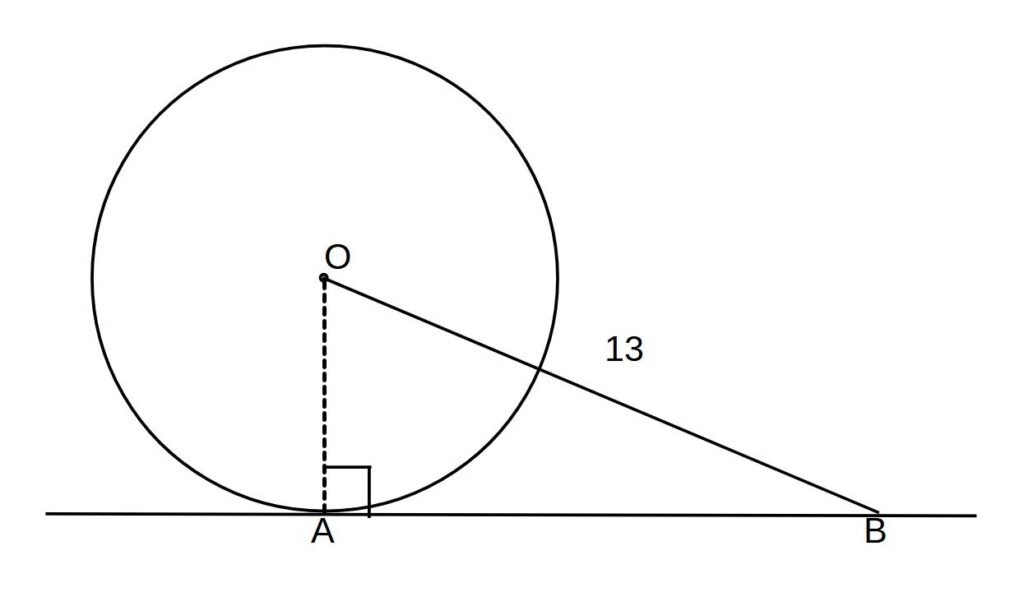
②半径5の円に接線をひき、
OB=13のときABの長さを求めよ。
接線と半径(復習)
円の中心と接点のキョリは最短(半径)となるから垂直(90°)になる!
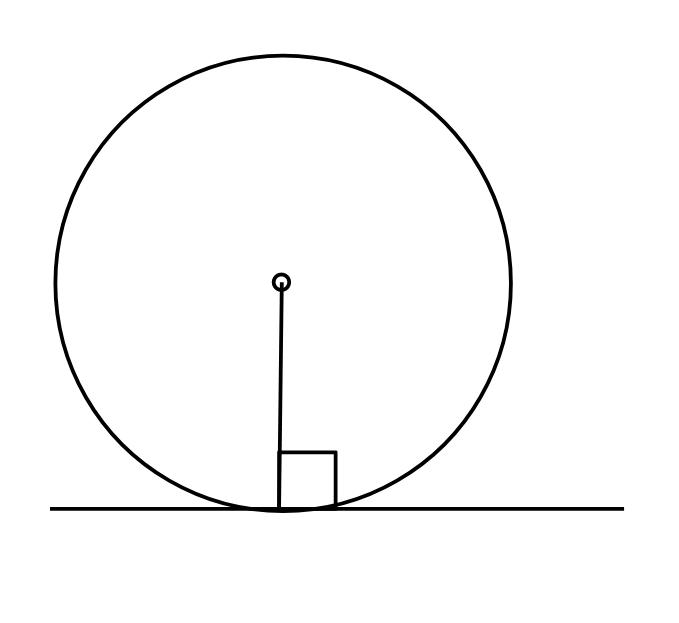
OB2=OA2+AB2
132=52+AB2
169=25+AB2
AB2=144 AB>0
AB=12
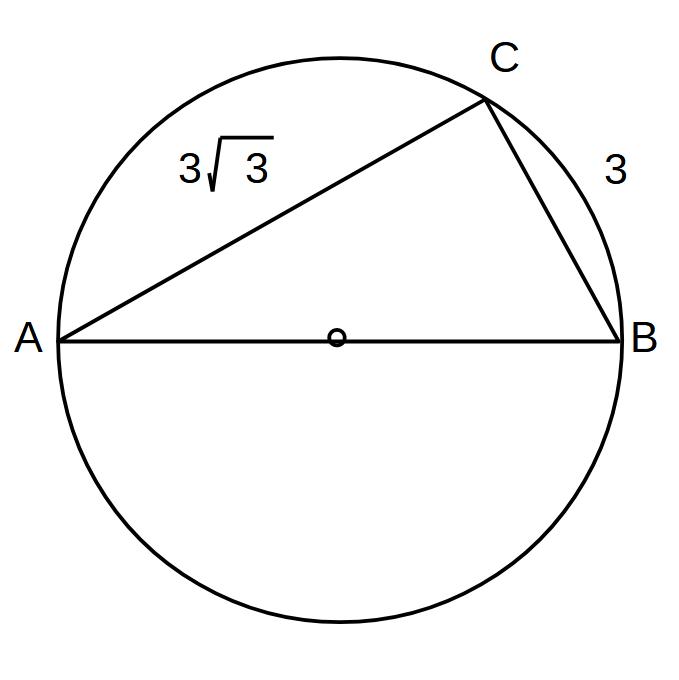
③AC=33、CB=3のとき、円の半径を求めよ。
∠ACB=90°(円周角)
AB2=AC2+CB2
AB2=27+9
AB2=36 AB>0
AB=6
半径=3

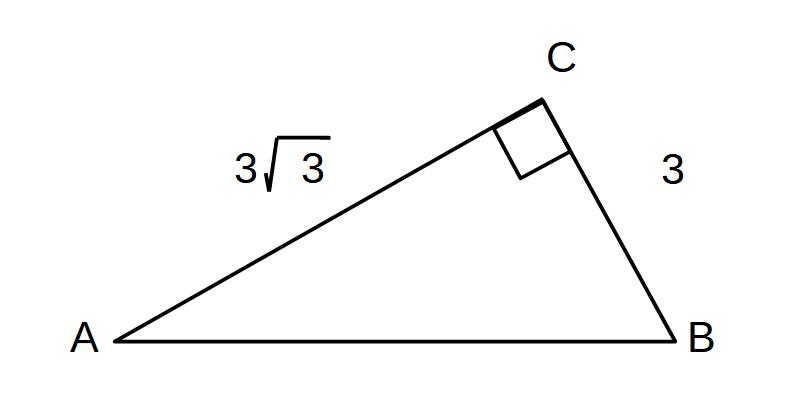
(応用)CからABまでの距離
※相似を利用する
AC:CD=AB:BC
3√3:CD=6:3
6CD=9√3
CD=3√3/2