(1)直方体への応用
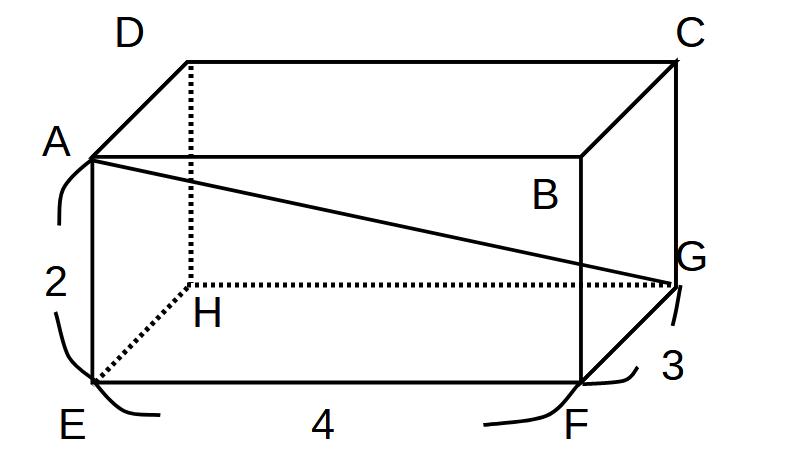
AGの長さを求めよ。
※空間を、平面で切り取って考える!
→辺AGを含む面を切り取る
=面AEGCができる
図の直方体を辺AGを含んだ辺面で切り取る
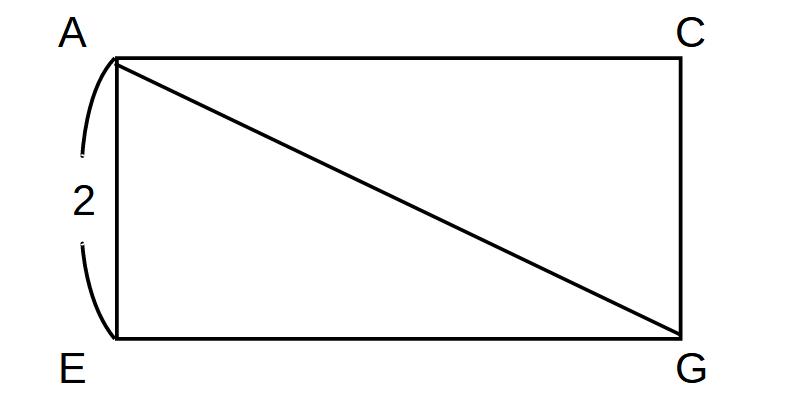
切り取った面だけを図示したもの。
※AGの長さを求めるには、EGの長さが必要!
・辺EGを含む面=面EFGHも切り取る
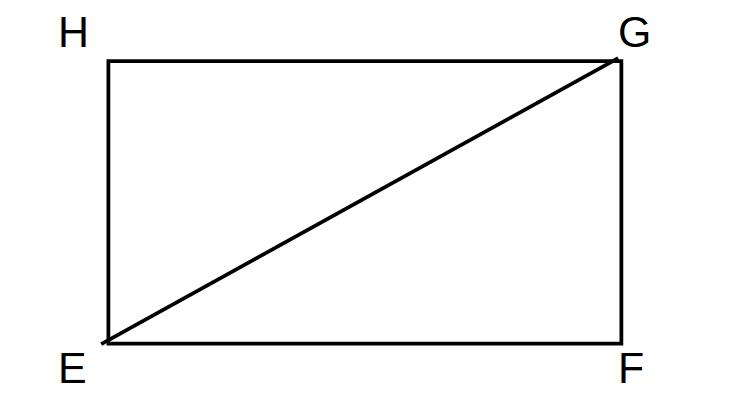
面EFGHの切り取った面
問題の図より、GF=3、EF=4
EG2=9+16=25
EG=±5 EG>0より
EG=5
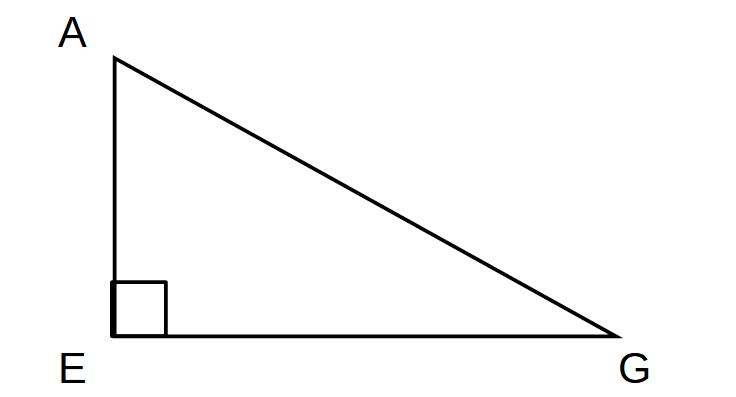
EG=5なので、△AEGで三平方の計算をする
AE=2、EG=5
AG2=4+25=29
AG=± √29 AG>0
AG=√29
(2)立方体への応用
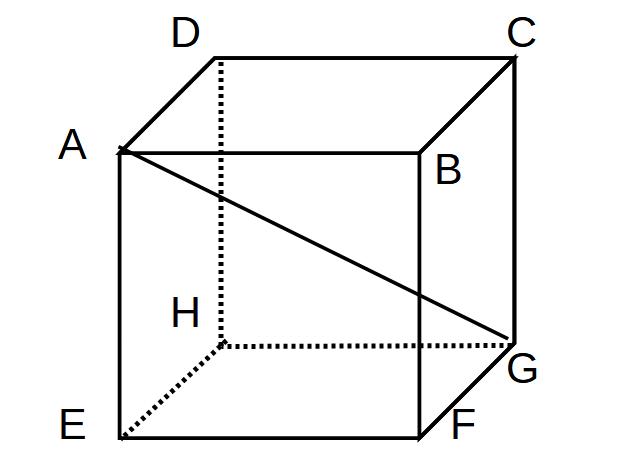
1辺6cmの立方体である。
AGの長さを求めよ。
※直方体の時と同様、平面を切り取って三角を作っていく!
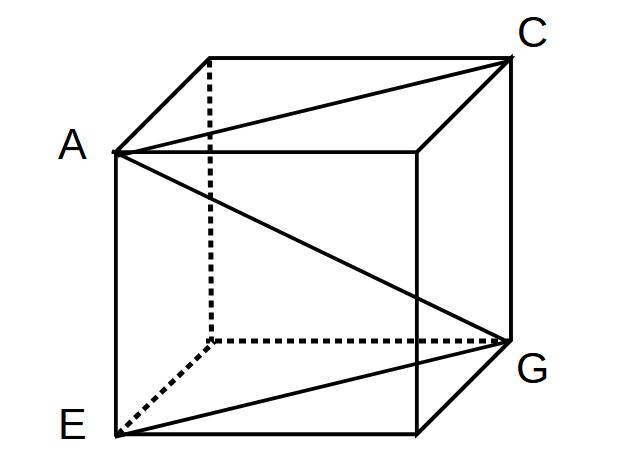
まずは辺AGを平面で切り取るために、AEGCを切り取る
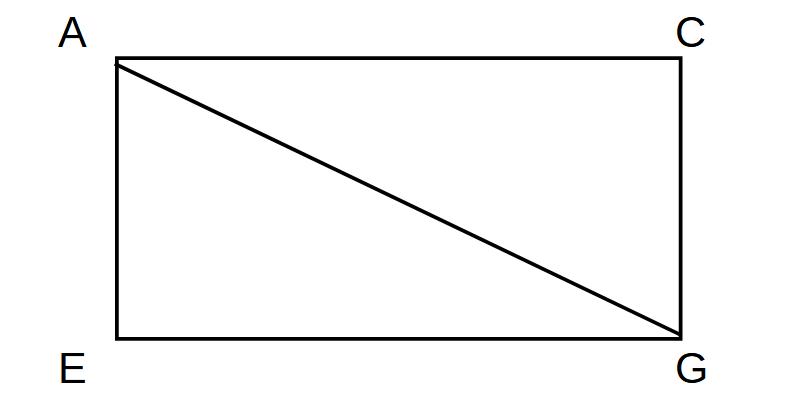
辺AGを求めるには、辺EGの長さが必要
→面EFGHの切り取りが必要!
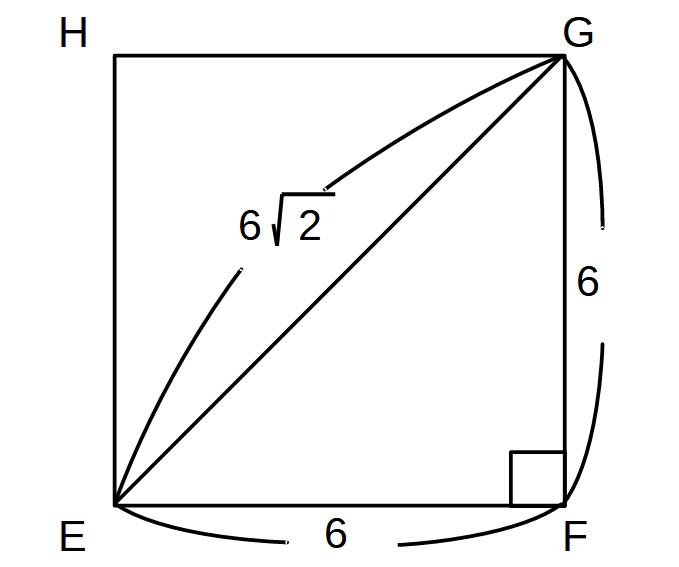
底面EFGHは、正方形
→直角二等辺三角形になり、1:1:√2の関係になる
→辺FG、辺EFはそれぞれ6なので、辺EGは6√2になる!
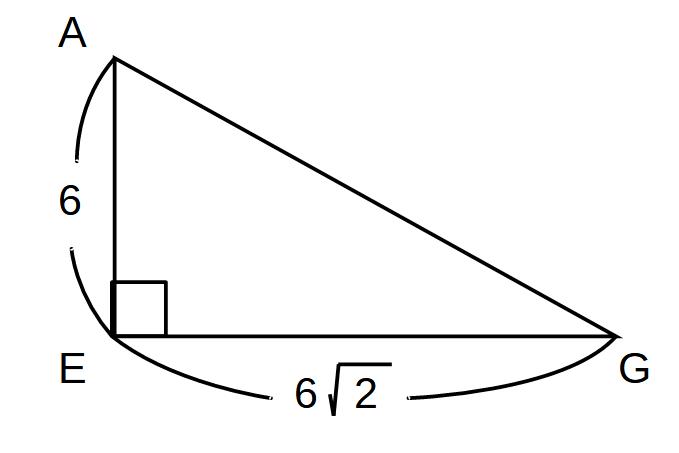
再び△AEGで計算
EG=6 √2より、△AEGで三平方の計算
AG2=36+72=108
AG=±6 √3 AG>0
AG=6 √3
(3)入試問題に触れる
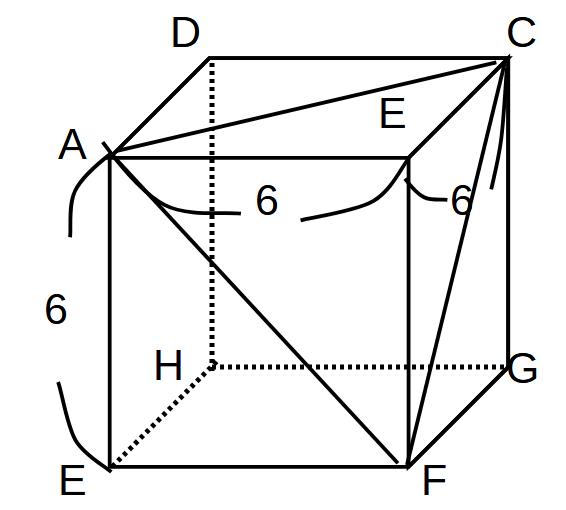
点Bから面ACFまでの距離を求めよ。
→体積の2通りの考え方を見ていきます
①底面=△ABCとして計算
=6×6×1/2×6×1/3
=36
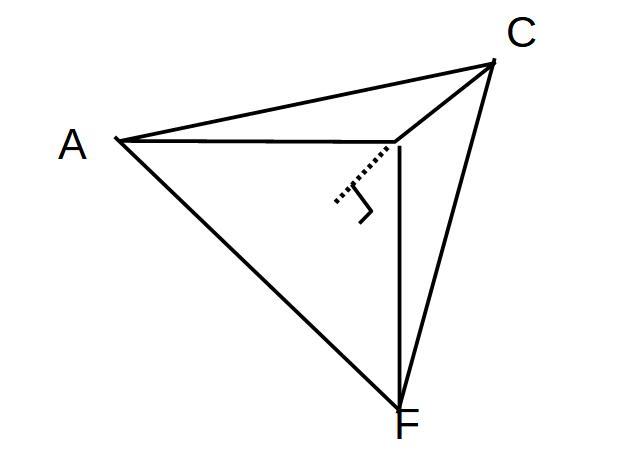
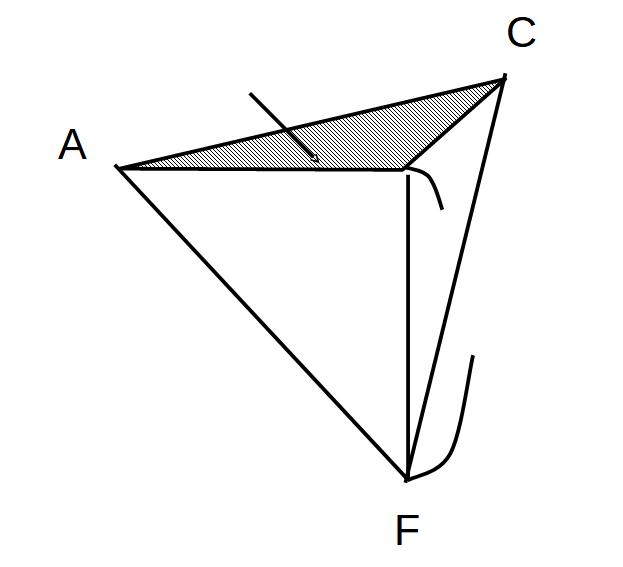
②底面=△ADFとしてみる
=B~ACFの距離=BHとする。

(△ACF)=正三角形
△ACF=6√ 2×3√ 6×1/2=18√3
=18 √3×BH×1/3=6√ 3×BH
①=②
36 =6√3×BH
bh=6/√3=2√3