(1)円すい
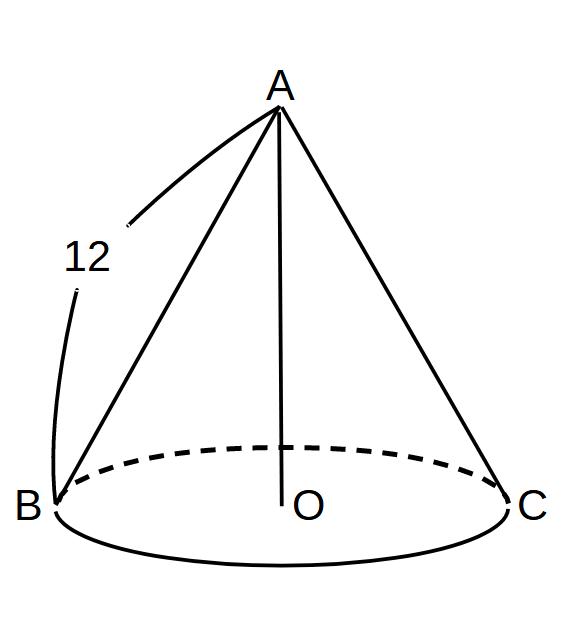
底面の半径=6のとき、円すいの体積を求めよ。
※高さを求めればOK
(高さの求め方)
⇒△ABOを切り取り、三平方の定理で計算
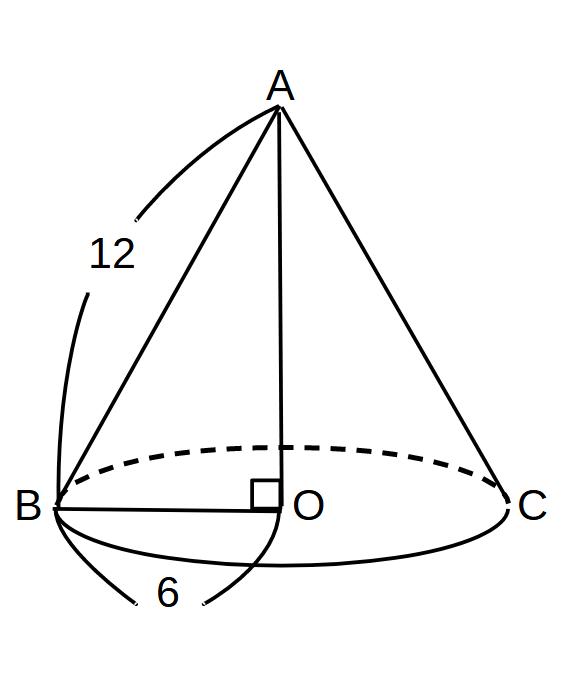
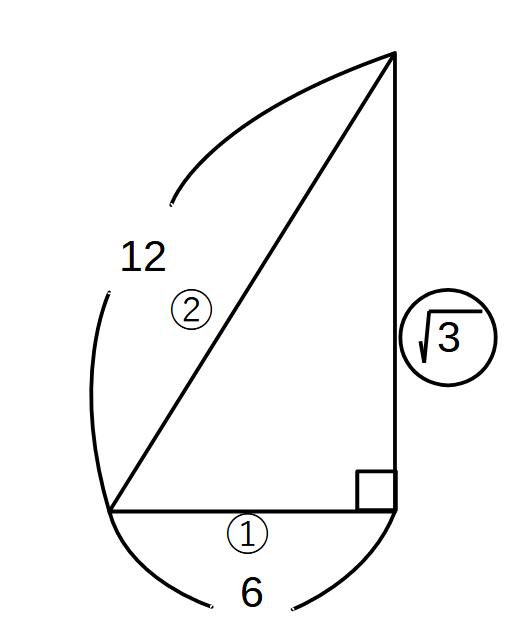
\(AO=6\sqrt{3}\)
\((1:2:\sqrt{3}より)\)
\( \displaystyle 6 \times 6 \times \pi \times 6 \sqrt{3} \times \frac{1}{3}=72\sqrt{3}\)
(2)円すいの内接球の半径
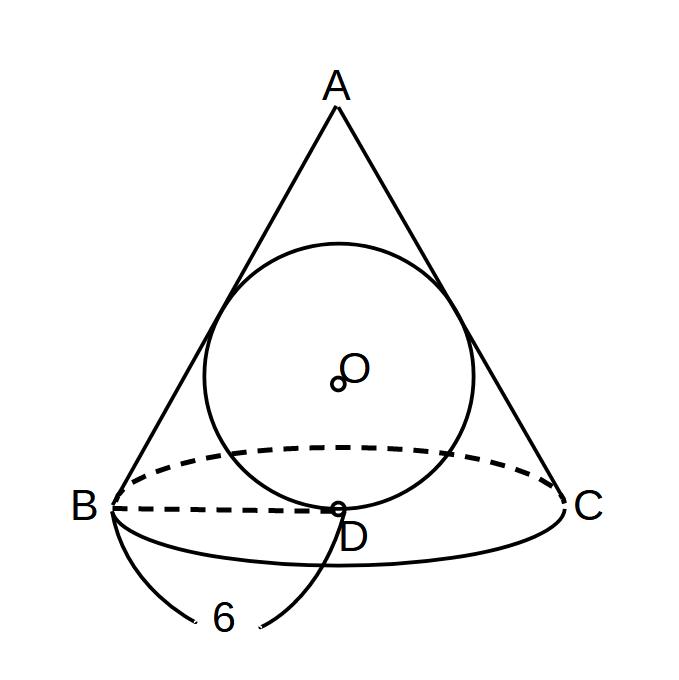
高さ=8の円すいに球が内接している。
球の半径を求めよ。
※三平方の定理と相似を使って求める!
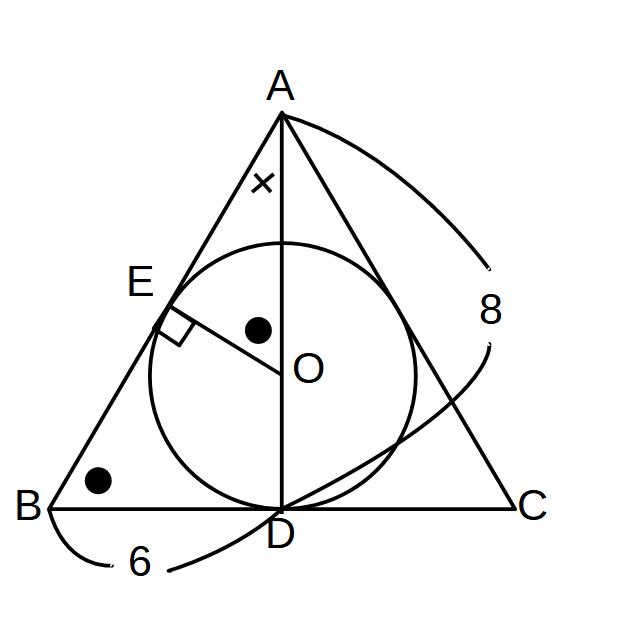
円すいの中心で半分に切断した図
→円(球)の中心Oから辺ABへ垂線を引き、接点をEとする。
すると、△ABD∽△AEOがわかる
AB2=64+36=100
AB=±10
AB=10
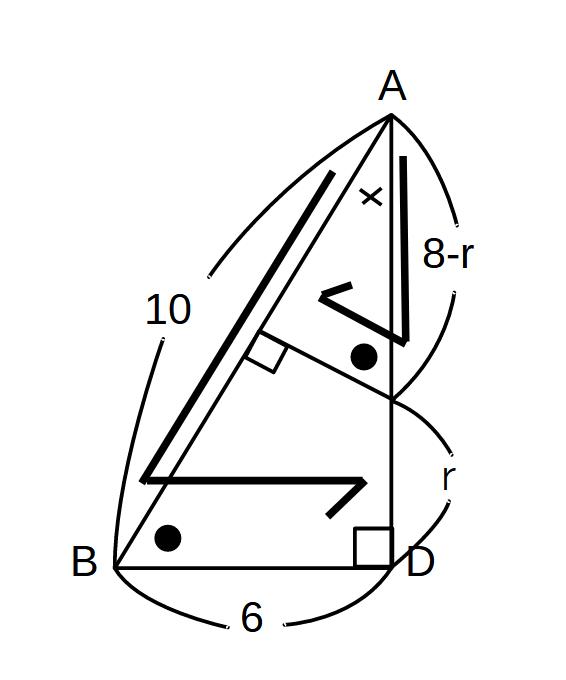
AB=10がわかり、△ABD∽△AEOがわかったので、相似の比を使って計算
8-r:r=10:6
6(8-r)=10r
48-6r=10r
-16r=-48
r=3
(別解)
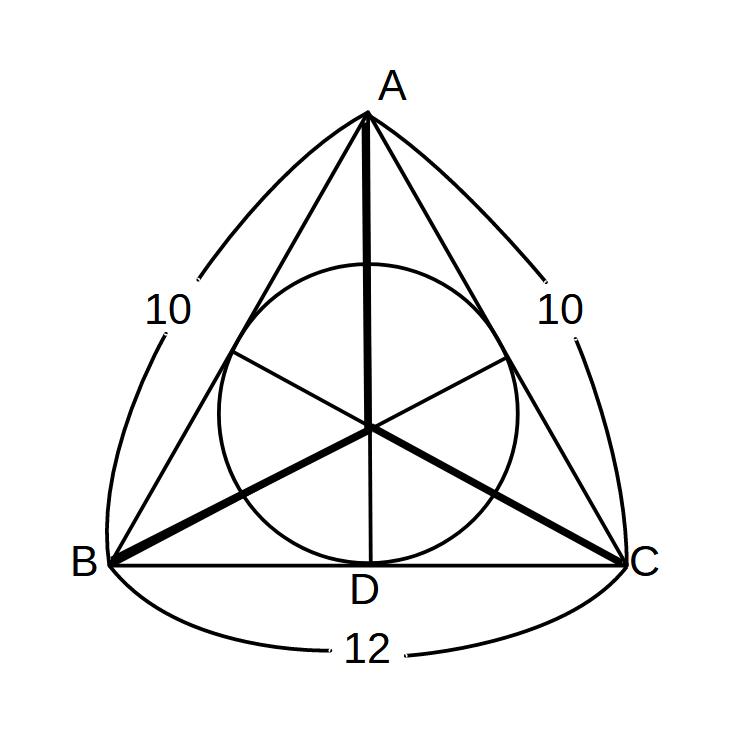
\( \displaystyle △ABC=12 \times 8 \times \frac{1}{2} =48 \)
△ABC=三角形3つ分
\( \displaystyle = \frac{1}{2}r(10+10+12)=16r\)
\(16r=48\)
\(r=3\)
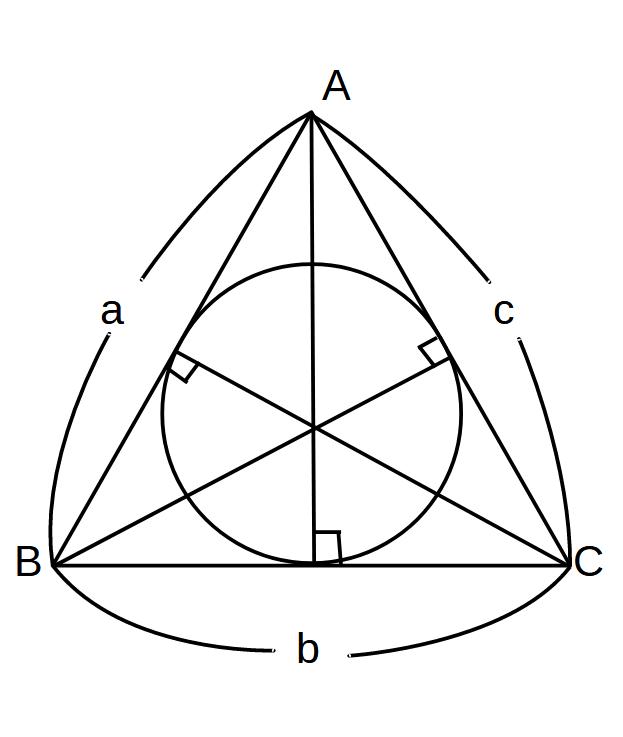
△ABC=Sとすると
\( \Large \displaystyle S= \frac{1}{2}r(a+b+c) \)
が成り立つ