今回は垂直二等分線について勉強します。
コンパスや定規を使って自分で作図等してみてください。
(1)中点…線分を2等分する点
(2)垂直二等分線…ある線分の中点を通り、その線分に垂直な直線
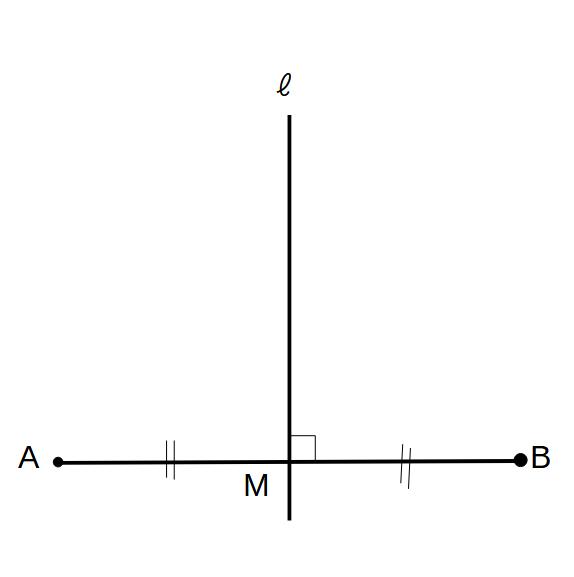
AM=MBなので、
Mは線分ABの中点
直線ℓは中点Mを通り
ABに垂直
→直線ℓはABの垂直二等分線
(3)垂直二等分線の作図
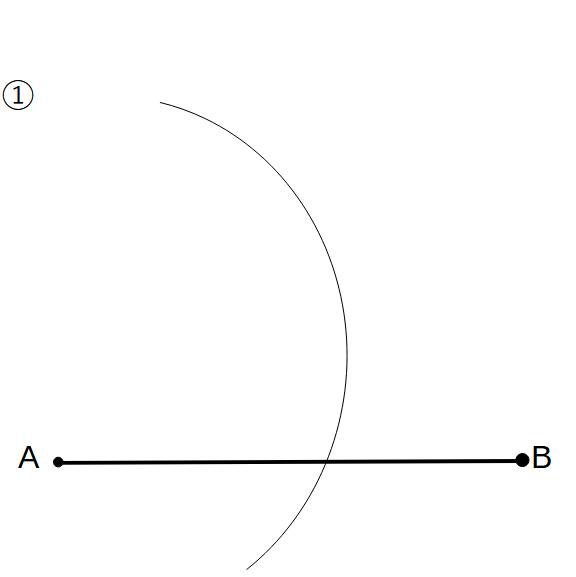
①点Aを中心に適当な大きさの円を書く
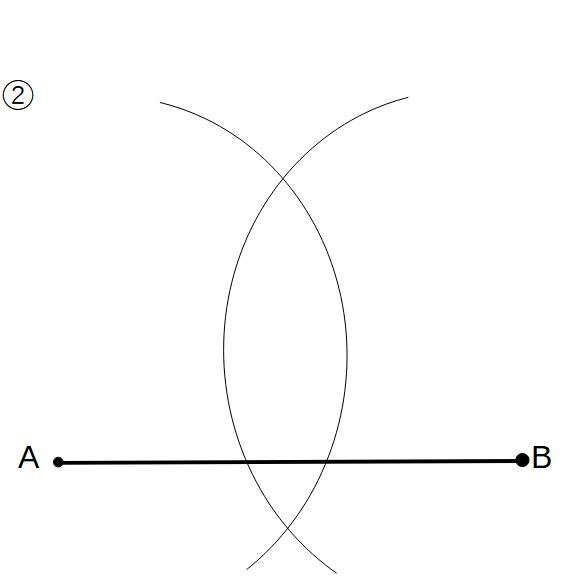
②点Bを中心に①と半径の等しい円を書く
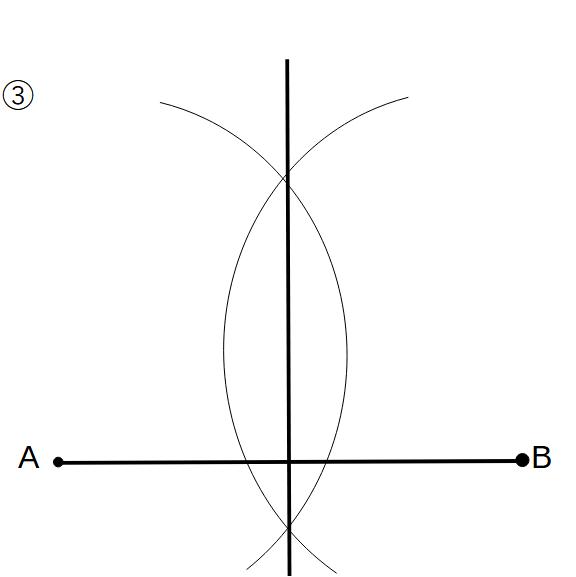
③①と②の円の交点2つを結ぶ直線を引く
※垂直二等分線は、ある線分を2等分する
→その線分の中点を通る
ある線分ABの垂直二等分線上の点は常に線分ABの両端から等しい距離になる
例)下図のような円と接する三角形ABCがある。線分AB・BC・CAから距離が等しい点Pを作図せよ。
解)
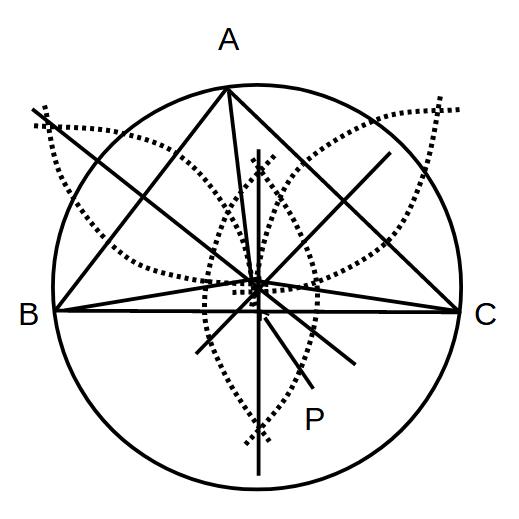
線分AB・BC・CAそれぞれの垂直二等分線をとり、その3つの垂直二等分線の交点Pが中心にとれる
※三角形の3つの辺(2つでもOK)の垂直二等分線は1点で交わる。この交点(Pと置く)と三角形の角頂点との距離はすべて等しい(垂直二等分線の交点だから)
→AP=BP=CP
つまり、三角形の3つの頂点を通る円を点Pを中心にして描くことができる。
このような三角形の3つの頂点を通る円を外接円(がいせつえん)といい、その中心Pを外心という。
例)弦の中点の作図
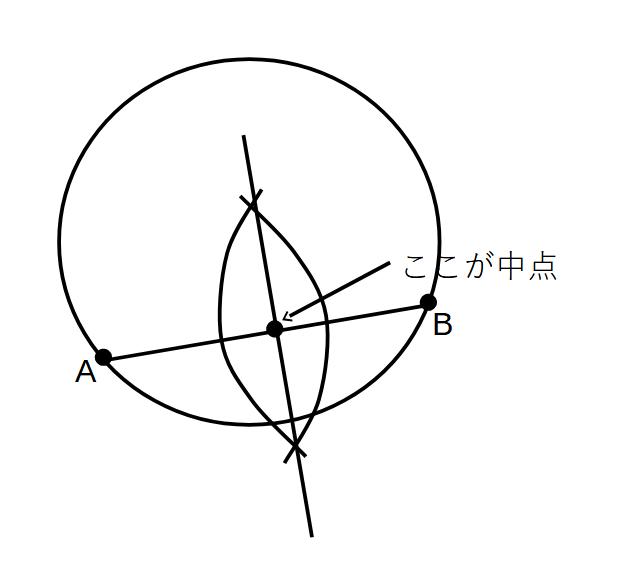
弦ABの中点を求めよ
→ABの垂直二等分線をひき、ABとの交点を中点とすればよい。
ちなみに、この状態は円の弦の二等分線を2本以上引いていくと、交わった点はその円の中心になるということを意味する。作図の問題の時に覚えておかなくてはなりません。このことを踏まえて次の例題を見てみましょう。
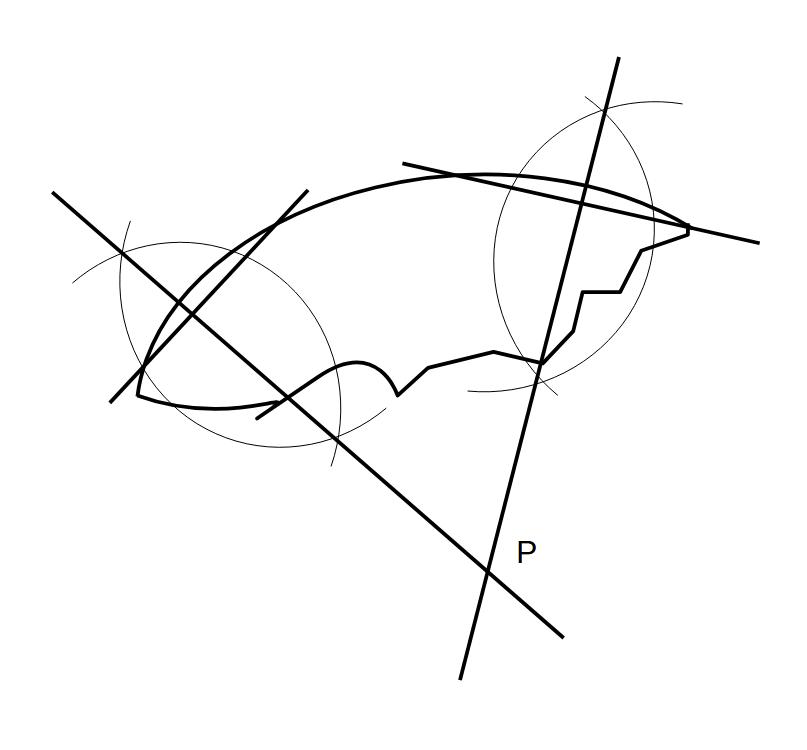
例)図のように割れた皿がある。
この皿の中心Pを作図せよ。
この皿のもともとの形は円形である。

解)皿はもともとは円であったということなので、
なので、残った弧から適当に弦を取り、垂直二等分線をひき、その交点が中心となる。
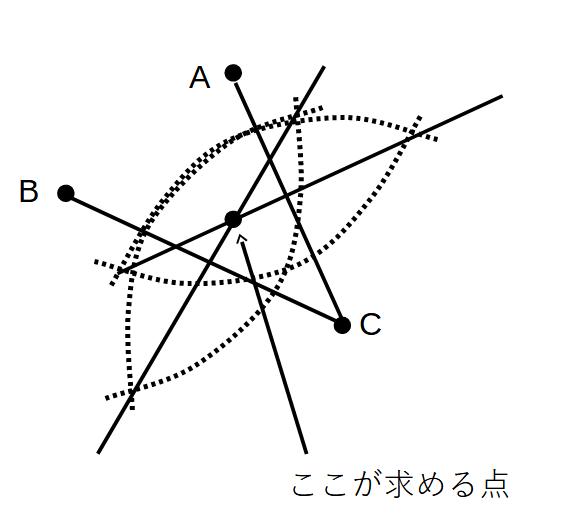
例)3点から等しい距離にある点Pの作図
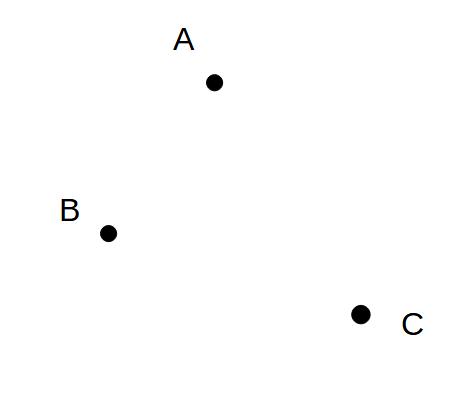
図の点ABCから等しい距離にある点Pを求めよ
解)
①AC、BC、CAのうち、2つに線を引き、そこから垂直二等分線をひき、2つの直線の交点を求める。
例)直線状にある2点と距離の等しい点
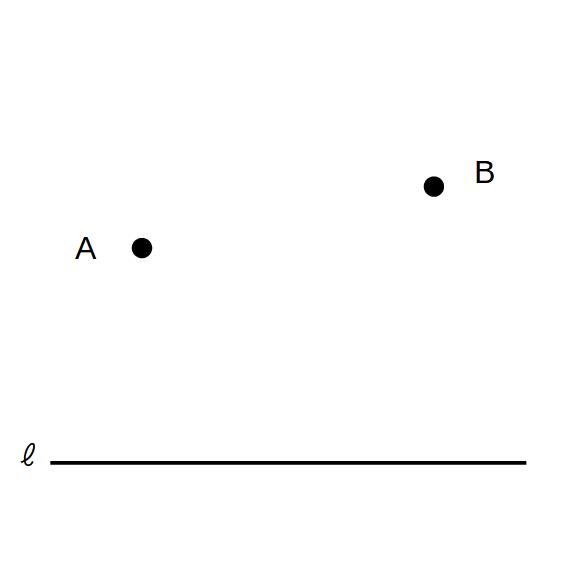
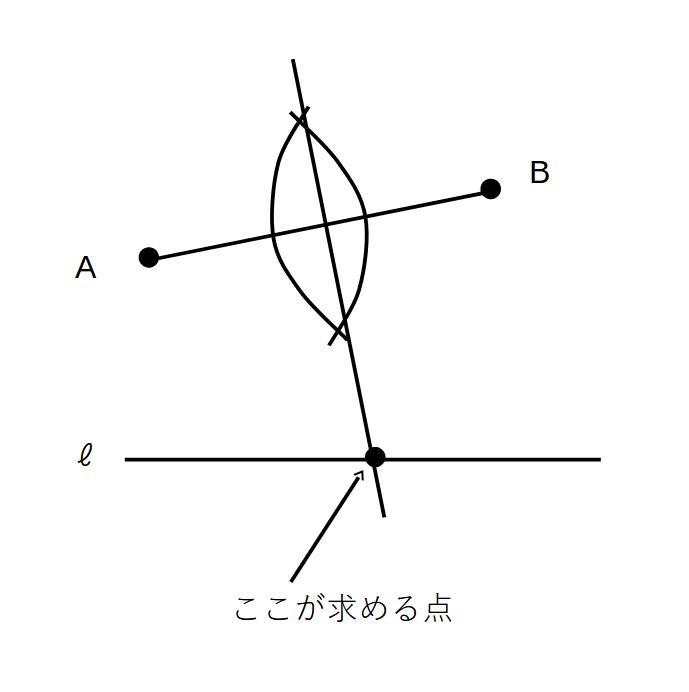
直線ℓ上にあって、2点A,Bからの距離が等しい点を求めよ。
解)
2点からの距離が等しい
→2点を線分の両端とする!
→垂直二等分線を引けばその上の点はすべて条件を満たす
→ℓとの交点を求めればよい
今回は2等分線を勉強しました。
作図がメインですので、決まり事をちゃんとふりかえり、類題をたくさん解きましょう。