今回は連立方程式の解き方について、さらにいろいろなパターンを勉強します。
いろいろな式が出てきますが、要するに、いかに代入法または加減法が使いやすいように式を作り替えるか、という考え方が重要になってきます。
(1)かっこのある連立方程式
例)
\begin{cases}x+2(y+4)=7…①\\
\\
3x-2y=1…②\end{cases}
まず、かっこのある連立方程式ですが、いままでの方程式の計算を勉強していれば、やり方はわかると思います。
まず、①のかっこをはずす計算をして式を整理してから、代入法・加減法を用いて連立方程式解いていく、という流れになります。
ひと手間増えただけですね。
まず、①のかっこをはずします。
x+2y+8=7
x+2y=ー1…①’ ←ここでダッシュをつけた式になります。
これを、加減法で計算します。ひっ算です。
xが求まりましたので、これを①か②に代入します。
①’でもいいですが、計算がややこしくなりそうなので、①か②にします。
①’ー②
\begin{array}{rr}
& x+2y=-1\\
-\big{)}&3x-2y=1\\
\hline
&4x=0\\
&x=0
\end{array}
今回は②に代入します。
代入して計算すると、答えが出ました。
\(-2y=1\)
\(\displaystyle y=-\frac{1}{2}\)
よって
\begin{cases}x=0\\
\\
\displaystyle y=-\frac{1}{2} \end{cases}
※今回は片方の式のみにかっこがありましたが、両方の式にかっこがあっても同じことで、まずはかっこをはずしてから連立方程式を解いていくという手順になります。
(2)小数を含む連立方程式
\begin{cases}0.2x+0.3y=0.9…①\\
\\
5x-3y=12…② \end{cases}
いかに代入法または加減法が使えるように式を作り替えるかということを考えていきます。
そうすると、とにかく①の小数がやっかいです。これをどうにかしてやりましょう。
→小数をなくすには?
①×10
2x+3y=9 …①’
※方程式は天秤で、両辺が釣り合っていればよいということを方程式のところで勉強しました。
これは方程式なので、両辺に10をかければ、すべて整数の式に作り替えることができます。
あとは、この①’と②を連立方程式として計算すればよいです。
今回は加減法で解きます。
xが求まりました。
①’ー②
\begin{array}{rr}
&2x+3y=9\\
+\big{)}&5x-3y=12\\
\hline
&7x=21\\
&x=3
\end{array}
②に代入します。
15-3y=12
3y=3
y=1
よって、x=3,y=1
(3)分数を含む連立方程式
次は、分数を含む連立方程式です。
小数の時と同じで、両辺に数をかけて分数を消去する、という流れですが、分数の場合は、分数が1つとは限りません。
分数が複数ある場合は、それらの最小公倍数を両辺にかける、といった方法(←方程式のところでやりました)を使います。
例)
\begin{cases}2x+y=6 …①\\
\\
\displaystyle \frac{4}{3}x+\frac{1}{2}y=6 …② \end{cases}
このように、分数が入っている場合は、分数を消去すべく考えます。
分母の最小公倍数を両辺にかけて分母をはらいます。
今回は②の両辺に6をかけます。
②×6
8x+3y=36 …②’
※もちろん、「両辺に」6をかけるので(方程式だから)、右辺の6にも6をかけます。忘れないように!
\begin{array}{rr}
&2x+y=6\\
+\big{)}&8x+3y=36\\
\hline
\end{array}
で、これからはいつものように連立方程式で加減法で…
といいたいところですが、よく見てください。
このままではxもyも消去できません。
ここからさらに、式を作り替える必要があります。
とりあえず、①に3をかけて、②’と同じにします。
①×3
6x+3y=18
これで、加減法で計算します。
これで、xが求まりました。
ここで、さらに代入して計算をします。
\begin{array}{rr}
&6x+3y=18\\
-\big{)}&8x+3y=36\\
\hline
&-2x=-18\\
&x=9
\end{array}
x=9を①に代入します。
18+y=6
y=ー12
よって、x=9,y=ー12
(4)比を使った式のある連立方程式
式の中に比を使った式があります。しかし、やり方さえ知っておけば今までとほぼ同じなので、恐れるに足りません。
例)
\begin{cases}x+2y=8 …①\\
\\
x:y=2:1 …② \end{cases}
②の式が比の式になっています。
いきなり見ると焦りますが、やり方さえわかれば怖くないです。
それではまず、比の性質からおさらいしましょう。
比は、=で区切った両側のうち、
左辺と右辺の内側(=側)
左辺と右辺の外側(=より遠目側)
同士でかけて、=でつなぐことができる
というものでした。
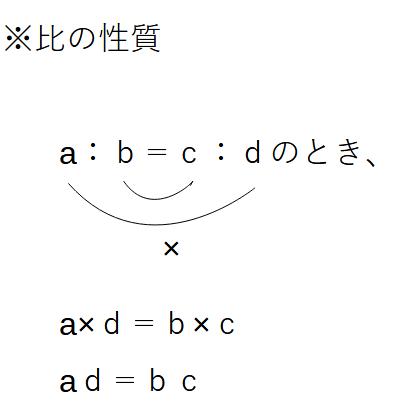
これさえ知っておけば、式を作り替えることができます。
②を計算
x:y=2:1 なので、
x=2y となり、
x-2y=0…②’
と置くことができます。
あとは、今までと同じ。
xがわかるので、これを代入します。
そうすると、y=2になります。
よって、x=4,y=2となります。
\begin{array}{rr}
&x-2y=0\\
+\big{)}&x+2y=8\\
\hline
&2x=8\\
&x=4
\end{array}
今回は、いろいろな連立方程式を解いてみました。
今までのやり方さえわかっていれば、それを用いて解いていくだけです。
が、いままでたくさん出てきたことをいっぺんに使う、ということもあり、うっかり忘れていてわからなくなった、解き方を忘れた、なんてことのないように、たくさん類題を解いて、身に着けていくようにしてください。