今回は「解が与えられている連立方程式」です。
実際に、例を見ていきましょう。

このように、問題文中に解がすでにあります。
しかし、よくみると、式にxとyだけでなく、aとbという文字まであります。
今回は、こういった問題の解法を勉強します。
※解き方
今回は、すでにxとyの値がわかっているので、xとyにはその数値を代入して式を整えたうえで、改めてaとbを導き出すための連立方程式として計算をすればよいだけです。
実際に、xとyに数値を代入していきましょう。
x=2,y=ー3を2式に代入すると、
→のようになります。
この形はただ単純にaとbを求める連立方程式なので、
あとは計算していくだけです。
\begin{cases}2a-3b=1 …①\\
\\
3a+2b=8…②\end{cases}
このままでは加減法で計算できないので、
①×2、②×3します。
それから計算すると、
aが出ました。
\begin{array}{rr}
& 4a-6b=2\\
+\big{)}&9a+6b=24\\
\hline
&13a=26\\
&a=2
\end{array}
a=2を①に代入
4-3b=1
3b=3
b=1
よって、a=2,b=1
このように、わかっている数を代入してしまえば、今までの連立方程式と同じになるので、連立方程式の形になるように問題文中から情報を拾って整えていく、という作業が必要です。
次は、ちょっとひねった問題です。
例)

今回は、「2組の連立方程式の解が等しい」ときのa、bの値を求める、という問題です。
解が等しい、ということは、(A)(B)の中のxはどちらの式でも同じ数値であるということです。同様にyもどちらの式でも同じ数値になるということです。
では、1つずつ見ていきましょう。
上の(A)(B)の2組の連立方程式を見てみると、(B)の方はxyだけでなくabがあり、そのまま回答するのは難しそうです。
しかし、(A)の方は普通の連立方程式になっており、計算すれば解答できそうです。
では、(A)から計算していきましょう。
実際に解いていくと、xの値が求まりました。
では、x=2を①に代入して、
10-4y=14 ∴y=ー1
x=2,y=ー1ということがわかりました。
\begin{array}{rr}
& 5x-4y=14\\
+\big{)}&6x+4y=8\\
\hline
&11x=22\\
&x=2
\end{array}
ここで、(A)と(B)両方の解が等しい、つまりxとyが同じであることが問題文に書いてあったので、(A)で出した上の答えを(B)に代入して計算すれば、aとbの数値が出るということになります。
このように、次はaとbを求める連立方程式を解いていきます。
計算の結果、a=1となりました。
これを代入して計算します。
2+b=ー1 ∴b=ー3
よって、a=1,b=ー3
\begin{array}{rr}
& 2a-b=5\\
+\big{)}&2a+b=-1\\
\hline
&4a=4\\
&a=1
\end{array}
つぎは、さらにちょっとひねります。
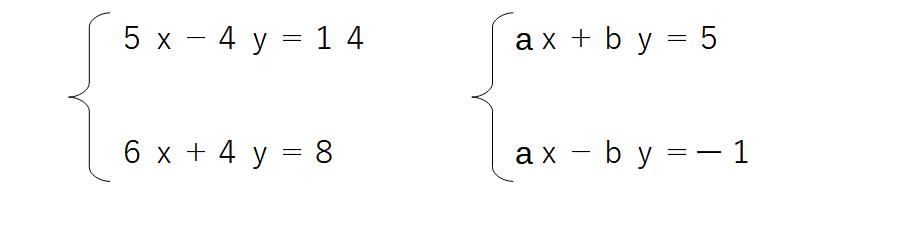
例)

さて今度は、さっきの問題とは式が同じようですが、先ほどとは打って変わって、順番が入れ替わっています。しかも、それぞれ(A)も(B)もそのままでは連立方程式の計算ができません。
こういった場合、どうやって解いていったらいいでしょうか。
※「2組の連立方程式の解が等しい」ということは、4つの方程式すべてに同じxとyが当てはまる、ということを意味しています。
つまり、式を入れ替えても全然OK、ということなのです。
だから、→のようにやってしまって問題ない、ということになります。
てことは、これはさっきやった問題と全く同じです。
今回は、解が与えられている連立方程式を勉強しました。
代表的なパターンをやりましたが、基本的に、すべての解が同じになること、入れ替えても問題ないこと等、法則を覚えておけば対応ができると思われます。
いろいろ問題を解いて、習得しましょう。